Расчет оптимальных режимов резания методом линейного программирования

В основе оптимизации режимов резания методом линейного программирования лежит построение математической модели, кото­рая включает совокупность технических ограничений, приведенных к линейному виду логарифмированием, и упрощенный вид целевой функции. Для решения этой задачи на ЭВМ могут быть использованы различные численные методы (метод перебора, симплекс-метод и др.), а также графический метод, наглядно представляющий мате­матическую модель процесса резания.

Следует отметить, что качество математической модели процесса резания металлов, и в первую очередь ее достоверность, зависит от выбора технических ограничений, которые в наибольшей степени определяют описываемый процесс. Наиболее важными ограниче­ниями являются следующие:

· режущие возможности инструмента;

· мощность электродвигателя привода главного движения;

· заданная производительность станка;

· наименьшая и наибольшая скорости резания и подача, допускаемые кинематикой станка;

· прочность и жесткость режущего инструмента;

· точность обработки;

· шерохо­ватость обработанной поверхности.

Рассмотрим особенности построения технических ограничений для наиболее распространенных методов обработки – продольного наружного точения и фрезерования торцовыми и цилиндрическими фрезами.

Ограничение 1. Режущие возможности инструмента. Это огра­ничение устанавливает связь между скоростью резания, определяе­мой принятой стойкостью инструмента, его геометрией, глубиной резания, подачей и механическими свойствами обрабатываемого материала, с одной стороны, и скоростью резания, определяемой кинематикой станка, с другой.

Скорость резания для различных видов обработки определяется по формуле

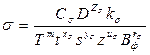(10.1)

где С_u – постоянный коэффициент, характеризующий нормативные условия обработки; D – диаметр обрабатываемой детали (или инструмента), мм; k_u– поправочный коэффициент, учитывающий качество обрабатываемого материала, состояние поверхности заго­товки, характеристику режущего инструмента; Т – принятая стой­кость инструмента, мин; m – показатель относительной стойкости; t – глубина резания, мм; s – подача, мм/об, мм/мин; г– число зубьев режущего инструмента; В_ф – ширина фрезерования, мм; х_u, у_u, u_u, z_u, r_u – показатели степеней или переменных в формуле скорости резания.

С другой стороны, скорость резания определяется кинематикой станка согласно зависимости

u = pDn× 10³ (10.2)

Приравнивая правильности формул (10.1) и (10.2) и сделав пре­образования, получают выражение первого технического ограни­чения в виде неравенства

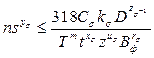(10.3)

Это техническое ограничение достаточно просто приводится к виду, описывающему конкретный вид обработки. Так, для продольного наружного точения можно получить, имея в виду значения коэф­фициентов z_u = 0, u_u = 0, r_u = 0, следующее неравенство:

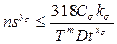
Ограничение 2. Мощность электродвигателя главного движения станка. Этим ограничением устанавливается взаимосвязь между эффективной мощностью, затрачиваемой на процесс резания, и мощ­ностью электропривода главного движения станка. Эффективная мощность, затрачиваемая на процесс резания при различных видах обработки, определяется по формуле

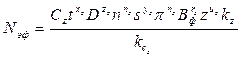(10.4)

где С_z – постоянный коэффициент, характеризующий условия обра­ботки; k_z – общий поправочный коэффициент на мощность, учиты­вающий изменение условий обработки против нормативных; 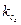– поправочный коэффициент, учитывающий отдельный вид обработки; x_z, z_z, п_{z ,} у_z, u_z, r_z – показатели 0 степени при t, D, n, s, z и В_ф. Учитывая необходимое условие протекания процесса резания, можно получить следующее неравенство:

N_эф £ N_nh, (10.5)

где N_n – мощность электродвигателя главного привода станка, кВт; h – КПД механизма передачи от электродвигателя к инстру­менту.

Приравнивая правые части выражений (10.4) и (10.5), полу­чаем второе техническое ограничение в виде неравенства

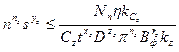(10.6)

Ограничение 3. Заданная производительность станка. Этим огра­ничением устанавливается связь расчетных скорости резания и по­дачи с заданной производительностью станка. Исходя из соотно­шения продолжительности цикла работы станка Т_ц, основного техно­логического t_o и вспомогательного непрерывного t_в.н времени, можно получить выражение для третьего технического ограничения

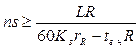, (10.7)

где R – заданная производительность станка, шт/мин; К_з – коэф­фициент загрузки станка; r_R – число деталей, обрабатываемых одновременно на одной позиции; L – длина рабочего хода инстру­мента, мм.

Ограничения 4 и 5. Наименьшая и наибольшая допустимые ско­рости резания. Эти ограничения устанавливают взаимосвязь расчет­ной скорости резания с кинематикой станка по минимуму и макси­муму. Они записываются в следующем виде:

n ³ n_{ст min}; (10.8)

n £ n_{ст max}. (10.9)

Ограничения 6 и 7. Наименьшая и наибольшая допустимые по­дачи. Эти ограничения аналогично двум предыдущим устанавливают взаимосвязь расчетной подачи с подачей, допустимой кинематикой станка по минимуму

s ³ s_{ст min} (10.10)

и максимуму

s £ s_{ст max}. (10.11)

Ограничение 8. Прочность режущего инструмента. Это ограни­чение устанавливает взаимосвязь между расчетными значениями скорости резания и подачи и допустимыми по прочности режущего инструмента. В основу построения этого ограничения закладывают условия нагружения режущего инструмента, например резца, как консольной балки с приложением на ее конце усилия, равного окруж­ной составляющей силы резания Р_z. В этом случае предел прочности материала державки резца при изгибе определяется зависимостью

s_и ³ М_изгk_з.п/W

где М_изг=Р_z l_в.р – изгибающий момент в месте закрепления дер­жавки резца на расстоянии l_в.р вылета резца от точки приложения окружной силы, кг/мм²; k_з.п – коэффициент запаса прочности; W – момент сопротивления сечения державки резца, мм².

Выражая окружную силу резания в зависимости от элементов режимов резания, а также учитывая форму державки (для прямо­угольного сечения шириной В и высотой H момент сопротивления равен 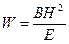) и значение предела прочности для незакаленной углеродистой конструктивной стали s = 20–24 кг/мм², можно получить после некоторых преобразований следующее ограни­чение:

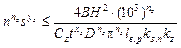(10.12)

Ограничение 9. Жесткость режущего инструмента. Это ограни­чение устанавливает взаимосвязь между расчетными значениями скорости резания и подачи и допустимыми по жесткости режущего инструмента. Известно, что максимальная нагрузка, допускаемая жесткостью резца Рж.доп, определяется по формуле

P_ж.доп = 3fEI/l³_в.р

где f – допустимая стрела прогиба резца, мм; Е – модуль уп­ругости материала резца (для конструктивной стали Е = (2–2, 5)·10⁴ кг/мм²); I – момент инерции державки рез­ца, мм⁴.

Величина допустимого прогиба резца f зависит от требуемой точности обработки и может быть принята для чернового и полу­чистового точения равной 0, 1 мм, а для чистового – 0, 05 мм. Момент инерции державки резца зависит от ее формы. Для прямоугольного сечения с шириной В и высотой H он определяется по формуле I = BH³/12. Из условия соотношений окружной составляющей Р_z и максимальной нагрузки, допускаемой жесткостью резца, и после соответствующего представления Р_z через элементы режима резания получают девятое ограничение в виде неравенства Р_z £ Р_ж.доп, а после подстановки значений

(10.13)

Ограничение 10. Жесткость заготовки. Это ограничение устанав­ливает взаимосвязь расчетных значений скорости резания и подачи с допустимыми. Из-за многообразия форм заготовок невозможно получить общие зависимости для описания рассматриваемого вида технического ограничения. Поэтому остановимся на его построении для точения цилиндрической гладкой заготовки и закрепления ее в центрах.

В основу этого ограничения положено условие, при котором величина прогиба у_с заготовки под действием радиальной состав­ляющей силы резания Р_у должна быть меньше или равна допустимому прогибу т.е. у_с £ у_доп.

Из рис. 10.1 видно, что допустимый прогиб долженбыть меньше величины допуска на размер: у_доп £ 0, 5 d, где d – допуск на раз­мер, мм. Величина прогиба заготовки

У_с = Р_ух²_р (L_з-х_p)² /ЗЕIL₃

где L_s – длина заготовки, мм; x_р – расстояние от правого торца до места приложения силы (до резца), мм; I = pD⁴_np /64 – момент инерции сечения заготовки в месте искомого прогиба, мм⁴; D_np – приведенный диаметр ступенчатого вала, мм.

После преобразования рассмотренных формул и подстановки в них значения

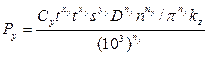
получим техническое ограничение по жесткости заготовки

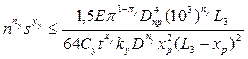(10.14)

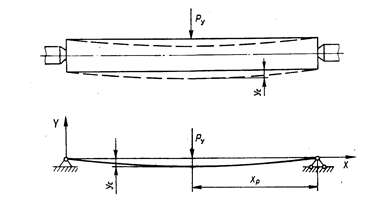
Рис. 10.1. Схема деформации заготовки при точении под действием радиальной составляющей силы резания

Ограничение 11. Прочность механизма подач станка. Это ограни­чение устанавливает взаимосвязь расчетных скоростей резания и подачи с допустимыми по прочности механизма подач станка. Имеет место обобщенная зависимость определения силы для различ­ных видов обработки

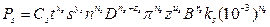
При продольном наружном точении коэффициенты z_s U_s, r_s равны нулю, а при фрезеровании коэффициент n_s = 0. В общем виде огра­ничение имеет вид P_s £ P_{s доп}. Значение P_{s доп} находят в паспортных данных металлорежущего станка. Подставив в это неравенство выражение для Р_s получим техническое ограничение по прочности механизма подач станка

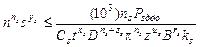(10.15)

Ограничение 12. Требуемая шероховатость поверхности. Это огра­ничение устанавливает взаимосвязь расчетных скорости резания и подачи с допустимыми по требуемой высоте или форме шерохо­ватости.

Известно, что выбор скорости резания и особенно подачи при получистовой и чистовой обработке очень часто определяется тре­буемой шероховатостью поверхности. В основу этого ограничения могут быть положены многочисленные экспериментальные зависи­мости для различных характеристик шероховатости поверхности R (Ra, Rz, Rmax), шага микронеровности Sm, величины опорной по­верхности tp, которые представляются в виде следующих выражений мультипликативного типа:

,

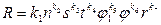где j₁, j, r – параметры геометрии режущей части инструмента; k₁, k₂, k₃,..., k₇ – экспериментально установленные коэффициенты.

После преобразования с учетом обеспечения требуемого значения шероховатости получают техническое ограничение также в виде неравенства

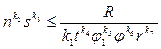(10.16)

Знак неравенства (10.16) определяется видом характеристики шеро­ховатости. В тех случаях, когда требуется одновременно обеспечить несколько характеристик шероховатости, рассматриваемое техни­ческое ограничение представляется в виде нескольких неравенств. Так, для обеспечения при наружном продольном точении заготовки из стали 45 шероховатости R_a и шага микронеровностей S_m могут быть использованы для построения технических ограничений сле­дующие зависимости:

;

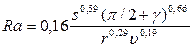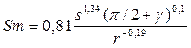
где g – передний угол резца.

Выбранные и описанные выше технические ограничения, отра­жающие с определенной степенью точности физический процесс резания в совокупности с критерием оптимальности, образуют мате­матическую модель процесса резания.

При определении режимов резания широкое применение для двух элементов n и s имеет метод линейного программи­рования, общая задача которого состоит в определении неотри­цательных значений переменных, удовлетворяющих системе огра­ничений в виде линейных равенств и неравенств и обеспечивающих наибольшее или наименьшее значение некоторой линейной функ­ции – критерия оптимальности.

Таким образом, первая задача, которая должна быть решена, – это приведение всех технических ограничений и оценочной функ­ции к линейному виду. Для примера рассмотрим приведение к линей­ному виду первого технического ограничения (10.3) методом лога­рифмирования:

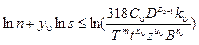(10.17)

Введя обозначения ln n = x₁, ln (100 s) = x₂,

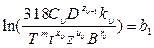
и подставив их в неравенство (10.17), получим

x_{1 +} у_u х₂ £ b₁ (10.18)

Аналогично могут быть получены в линейном виде зависимости для других технических ограничений.

Анализ ранее рассмотренных видов и критериев оптимальности показывает, что при оптимизации по двум элементам режимов реза­ния лих без изменения глубины резания, стойкости инструмента и других технических факторов эти оценочные функции при введении ряда упрощений выражаются через n и s достаточно просто. Так, для минимальной себестоимости операции можно записать С_оп = c/ (ns), где c₁ – постоянная величина, не зависящая от режимов резания n и s.

Из этого выражения видно, что значение оценочной функции является наименьшим, когда произведение ns максимальное. В этом случае при приведении оценочной функции к линейному виду можно получить

f₀ = (x₁ + х₂) ® max. (10.19)

Преобразование технических ограничений к линейному виду и представление их в виде системы неравенств в совокупности с оце­ночной функцией дает математическую модель процесса резания металлов

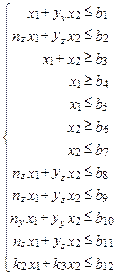(10.20)

Применительно к математической модели (10.19) – (10.20) зада­ча определения оптимального режима резания сводится к отысканию среди всевозможных неотрицательных значений х₁ и х₂ системы таких значений x_1опт и х_2опт, при которых линейная функция принимает максимальное значение f_{o max}.

Математическая модель процесса резания может быть изобра­жена в графическом виде. В этом случае каждое техническое огра­ничение представляется граничной прямой, которая определяет полуплоскость, где возможно существование решений системы неравенств. Граничные прямые, пересекаясь, образуют многоуголь­ник ABCDEF, внутри которого любая точка удовлетворяет всем без исключения неравенствам. Поэтому этот многоугольник принято называть многоугольником решений (рис. 10.2).

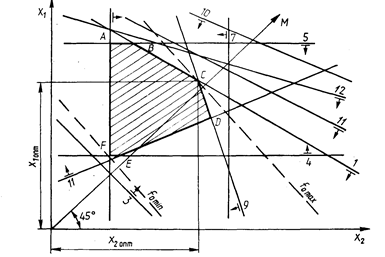
Рис. 10.2. Графическое изображение математической модели процесса резания

Теория линейного программирования показывает, что экстре­мальное значение оценочной функции (при выпуклом многоуголь­нике решений) обеспечивается для х₁ и х₂, находящихся в точке, лежащей на одной из граничных прямых или их пересечении.

Поэтому задача отыскания оптимальных значений x_1опт и x_2опт сводится к последовательному вычислению координат всех возмож­ных точек пересечения граничных прямых и затем определению для них наибольшей суммы

f₀ = (x₁+х₂) _max.

После определения координат x_1опт и x_2опт вычисляют оптималь­ные значения элементов режима резания по формулам:

n_опт = exp (x_1опт);

s_опт = exp (x_2опт) / 100.

Для определения оптимального решения задачи, заданной систе­мой линейных уравнений и неравенств, обычно используется метод полного перебора точек, образующих выпуклый многоугольник возможных решений. Определяются попарно точки пересечения прямых и подставляются координаты этих точек в неравенства системы. Точка, координаты которой удовлетворяют всем без исклю­чения прямым (проверка на совместимость системы уравнений) и одновременно сумма координат которой (x₁+х₂) является наиболь­шей, и будет точкой оптимума.

Последовательность решения задачи следующая.

1. Рассматривается пара прямых и производится их проверка на параллельность.

2. Если прямые параллельны, то рассматривается следующая пара, а если нет, то определяются координаты x₁ и х₂ точки их пере­сечения.

3. Проверяются знаки координат. Если координаты положи­тельны, то путем подстановки в каждое из неравенств найденных значений x₁ и х₂ определяют, находится ли точка в области возмож­ных решений. Если хотя бы одно из неравенств не удовлетворяется, то эта точка отбрасывается и проводится такой же анализ следую­щей пары.

4. Если x₁ и х₂ положительны и удовлетворяют всем без исклю­чения неравенствам, то определяется сумма координат t_о= x₁+х₂ и запоминается в виде некоторого значения А. Все вышеописанные действия производятся до тех пор, пока не будут рассмотрены все пары прямых.

5. В случае противоречивости исходных данных может оказаться, что области возможных решений нет. Признаком несовместности системы является равенство нулю величины А, которая в противном случае равна сумме координат x₁+х₂, являющихся решением задачи.

6. Если решение находится на прямой, параллельной прямой оценочной функции, то в качестве решения принимаются координаты той точки, у которой больше координата х₂ (т. е. при большем зна­чении подачи).

7. Если система неравенств совместна и найдена точка, сумма координат которой x₁+х₂ является наибольшей, то опти­мальная частота вращения n = 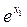и оптимальная подача s= 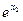/100.

Эта же задача может решаться графически. Оценочная функция f₀ = x₁+х₂ изображается прямой, перпендикулярной к вектору максимизации M (рис. 10.7). Так как направление вектора M есть на­правление возрастания линейной функции f₀, то следует ожидать, что в первой точке касания F с многоугольником решения она примет минимальное значение f_0min, а в последней точке С – максимальное значение f_0max. Следовательно, вершина многоугольника решений С является точкой оптимума, а ее координаты Х_1с и Х_2с – оптималь­ным решением системы.