Равносильные формулы в исчислении предикатов.

Исчисление предикатов это расширение исчисления высказываний. Все идет по аналогии.

В исчислении предикатов мы говорили, что формулы φ ₁ и φ ₂ являются равносильными, если они принимают одинаковые значения при одинаковых значениях переменных.

2 формулы Ф₁ и Ф₂ в исчислении предикатов являются равносильными, если они принимают одинаковые значения при одних и тех же значениях логических переменных (типа 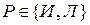), связанных (типа 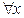и 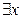), свободных переменных и при одних и тех же значениях кванторов, т.е. при (равносильных кванторах) одноименных кванторах.

P(x, y)↔ [x> y]

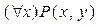– здесь x – связанная, а y – свободная переменные.

.

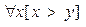Поскольку в определении равносильности функции в ИП вложено понятие равносильности функции в ИВ, то равносильные формулы, рассмотренные в ИВ, автоматически входят в равносильные формулы в ИП.

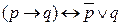(ИВ), т.е. φ ₁↔ φ ₂.

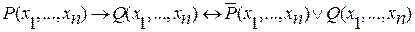
(ИП).

Все остальные формулы переносятся аналогично. За счет кванторов мы расширяем тот список в ИП.

1)

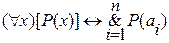
2)

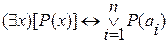
рассмотрим формулы Де Моргана в исчислении предикатов.

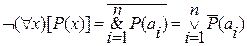
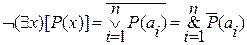
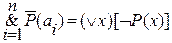
Запишем полученные формулы.

3)

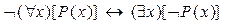
4) 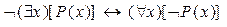– это аналоги функций Де Моргана в алгебре исчисления предикатов.

Для того, чтобы получить отрицание выражения начинающегося с квантора общности или существования необходимо сделать следующее:

1. над всеми связанными переменными необходимо поменять кванторы (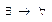 и наоборот).

2. знак отрицания вынести перед предикатом.

Пример:

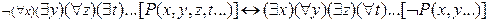
Пример:

{a₁, a₂,...a_n,...}

1. 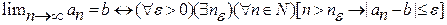Но часто последовательность не имеет предела |=> наше условие не выполняется, отрицается.

2.

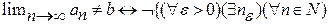
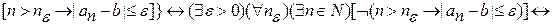
{по свойству 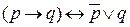, то 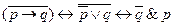} тогда получим выражение:

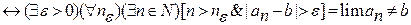
5)

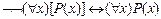
6)

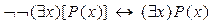
7)

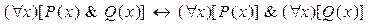
8)

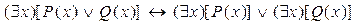
9)

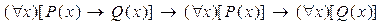
10)

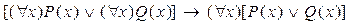
11)

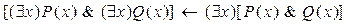
12)

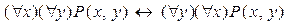
13)

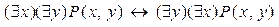
14) 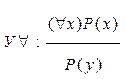, У – удаление квантора обязность.

15)

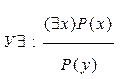
16)

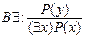
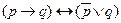
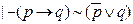
В предыдущих 13 формулах знак (↔) можно заменить на знак (~), получим отдельную формулу, которая является тождественно-истинной.

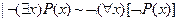
1. любое целое число есть рациональное

2. 1 – целое число.

=> 1 – рациональное число.

1-ое выражение перепишется

1.

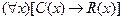
C–целые, R–рациональные.

2. С(1)

R(1)=?

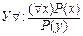
Заключение в том, что имеющееся свойство P(x) конкретизуется для определенного значения y.

1.

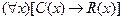
2. C(1)

3. C(1)→ R(1)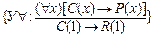

4. R(1) {ПО: 2, 3}