Математическое описание физико-химических и тепловых процессов в промышленных технологиях.

Классификация исследуемых объектов управления. Объекты автоматизации можно классифицировать в зависимости от вида регулируемой величины (температуры, давления, расхода и т. д.); по характеру материальных и энергетических внутренних связей в них: механические, гидравлические, тепловые, диффузионные, химические и др. различают также объекты с одной и несколькими регулируемыми величинами. Однако такая классификация не отражает статических и динамических свойств объектов. В зависимости от динамических свойств различают объекты с сосредоточенными и распределенными параметрами.

Объектами с сосредоточенными параметрами называют такие, в которых в состоянии равновесия регулируемые величины практически имеют одинаковые значения по всему объему объекта. В переходном режимы в любой точке такого объекта характер изменения регулируемых величин одинаков в одно и тоже время. Примером могут служить тепловые объекты, в которых температура в жидкости определенного объема одинакова во всех точках, если она хорошо перемешивается; объекты типа емкостей, в которых регулируемой величиной является давление газа, и т. д.

Объектами с распределенными параметрами называют такие, в которых значения регулируемых величин в различных точках объекта неодинаковы (например, давление вещества в трубопроводе по его длине при транспортировки, температура продукта в трубчатом нагревателе по его длине).

Для математического описания объектов с сосредоточенными параметрами обычно достаточно обыкновенных дифференциальных уравнений, а для описания объектов с распределенными параметрами необходимы уравнения в частных производных.

Объекты с сосредоточенными параметрами в свою очередь можно подразделить на простые и сложные. К простым относятся объекты, динамические свойства которых описываются уравнениями элементарных типовых динамических звеньев, т. е. дифференциальными уравнениями, порядок которых не выше второго. Объекты, для описания динамических свойств которых необходимо применение дифференциальных уравнений более высоких порядков, относятся к сложным.

Почти все технологические процессы нефтепереработки и нефтехимии относятся к сложном объектам автоматизации с сосредоточенными параметрами или к объектам с распределенными параметрами.

Однако во многих случаях их можно рассматривать в виде системы, состоящей из большего или меньшего числа относительно простых объектов, соединенных между собой тем или иным образом. Поэтому в первую очередь представляет интерес рассмотрение простых объектов.

Рассмотрим математическое описание простых объектов с сосредоточенными параметрами. Технологические процессы, протекающие в объектах, можно представить в виде таких операции, как поступательное или вращательное движение, нагревание и охлаждение вещества в определенном объеме, перемешивание веществ, заполнение или опорожнение сосуда веществом и т. д. Такие процессы в большинстве своем характеризуются одной выходной (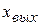) и одной входной (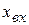) величинами, имеют одну степень свободы, и могут быть описаны обобщенным уравнением вида

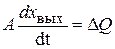, (11.1)

где 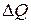- материальное или энергетическое воздействие на объект, а величина 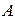характеризует динамические свойства объекта и определяет характер изменения 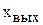во времен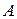и. и 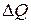для каждого из рассматриваемых процессов имеют конкретные выражения.

В таблице 10.1 приведены уравнения для различных единичных процессов, облегчающие составление математического описания самых разнообразных объектов.

В общем случае 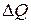равно разности между притоком 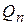и расходом 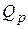вещества или энергии в объекте, т. е.

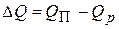(11.2)

В состоянии равновесия, как известно, воздействие на объект отсутствует, т.е. 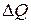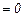. При А, отличном от нуля,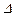 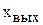также должно быть равно нулю. С появлением 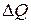в объекте возникает переходный процесс, в котором 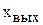изменяется во времени. Характер этого изменения определяется решением дифференциального уравнения (11.1)

Рассмотрим несколько примеров. Пусть имеется объект-емкость, характеризующаяся притоком газа 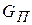и расходом 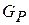, в которой предполагается регулировать давление 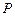(см. рисунок 11.1).

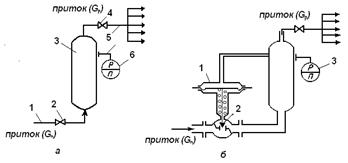
Рисунок 11.1 - Схемы ручного регулирования давления газа в аккумуляторе (а) и системы автоматического регулирования давления (б )

Таблица 11.1

Уравнения единичных процессов

Процесс	Дифференциальное уравнение	Принятые обозначения
Поступательное движение		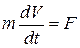t - время m - масса V - скорость F - результирующая сила
Вращательное движение		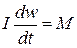I – момент инерции w – угловая скорость M – результирующий момент
Заполнение (опорожнение) сосуда жидкостью		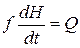f – площадь уровня H – высота (уровень) Q – объемный расход
Заполнение (опорожнение) сосуда газом		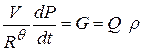V – объем сосуда P – давление газа Q - объемный расход ρ – плотность газа G – массовый расход R – газовая постоянная θ – абсолютная температура
Нагревание (охлаждение) тела		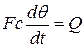F - вес c – удельная емкость θ – температура Q – тепловой поток
Сушка (увлажнение) тела		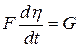F – вес абсолютно сухого вещества η – относительная влажность на абсолютно сухой вес G – вес поступающий (удаляемый) влаги за единицу времени
Растворение или осаждение из раствора (суспензии)		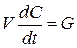V – объем растворителя C – концентрация растворенного вещества (в весовых единицах, отнесенных к единице объема) G – поступление (удаление) сухого вещества (по весу) в единицу времени
Выпаривание		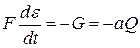F - вес растворенного абсолютно сухого вещества ε – отношение весов растворителя и растворенного вещества, т. е. величина, обратная весовой концентрации G – количество пара, образующегося в единицу времени a – коэффициент пропорциональности Q – количество тепла, проводимого в единицу времени

Для равновесного состояния имеем:

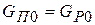(11.3)

где 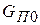и 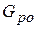- значение массовых расходов газа на линиях притока и потребления, соответствующие неизменному значению давления в емкости.

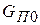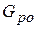В процессе работы объекта условие (11.3) может нарушаться в результате изменения по тем или иным причинам и . При 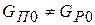количество газа m в емкости за бесконечно малый отрезок времени изменится на величину

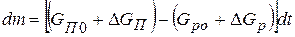. (11.4)

С учетом уравнения (11.3) перепишем выражение (11.4) в виде:

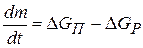. (11.5)

Согласно уравнению Клапейрона

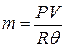, (11.6)

где Р - давление газа; V - объем емкости; θ - абсолютная температура газа в емкости; R - газовая постоянная.

Считая, что процесс изменения давления газа происходит без изменения его температуры, и продифференцировав выражение (11.6) по t, получим:

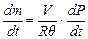. (11.7)

Подставляя уравнение (11.7) в выражение (11.5), будем иметь:

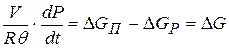. (11.8)

Сравнивая полученное выражение с уравнением (11.1) видим, что

.

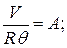
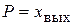При постоянном давлении газа, поступающего в емкость, 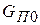зависит от степени открытия органа, управляющего притоком проходного сечения 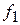и давления Р, т.е.

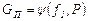. (11.9)

Расход газа 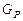, уходящего из емкости, зависит от давления P и от потребления, которое можно выразить как функцию проходного сечения 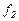органа управления расходом, т.е.

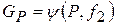. (11.10)

Зависимости (11.9) и (11.10) нелинейные. Линеаризуем их разложением в ряд:

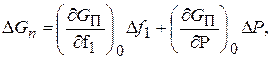(11.11)

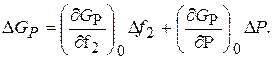(11.12)

Подставив зависимости (11.11) и (11.12) в уравнение (11.8) получим:

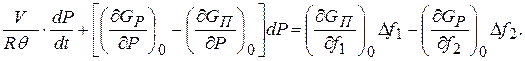(11.13)

Разделив полученное выражение на коэффициент при 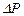и принимая во внимание, что

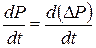
будем иметь:

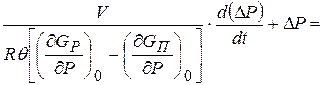
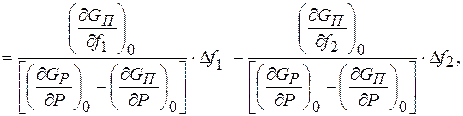
или

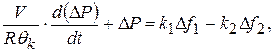(11.14)

где

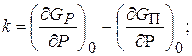
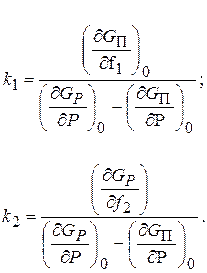
При неизменном 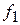уравнение (11.14) принимает вид:

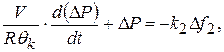
а при постоянном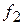

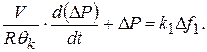
Обозначив Т через 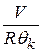запишем уравнение (11.14) в виде

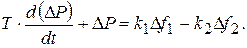(11.15)

Значения 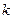, 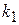и 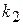находят из статических характеристик объекта (11.1) и уравнений расхода.

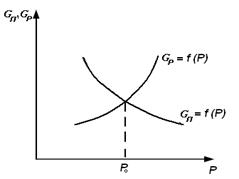
Рисунок 11.2 Статические характеристики объекта регулирования давления

При протекание жидкости, газа или пара через клапан зависимость между массовым расходом, отверстием истечения и перепадом давления на клапане выражается формулой

,

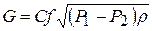где С - постоянный коэффициент; f - сечение истечения; P₁ и Р₂ –соответственно давление до и после клапана; ρ - плотность протекающий среды.

В нашем случае

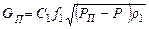; (11.16)

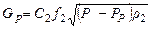, (11.17)

где Р_П и Р_Р - давление газа до сечения f ₁ и после сечения f₂; P -давление в емкост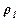и; и 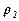– соответственно плотность газа до сечения и в емкости.

Продифференцировав уравнение (11.16) по f ₁, а уравнение (11.17) по f₂, получим:

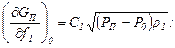(11.18)

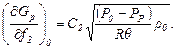(11.19)

Продифференцировав зависимости (11.16) и (11.17) по Р, будем иметь

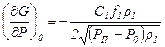; (11.20)

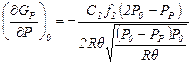. (11.21)

При дифференцировании уравнения (11.17) вместо 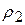подставляем 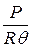. Из выражений (11.18) - (11.21) находят значение коэффициентов 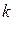, 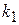и 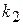.