
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекция 13 Примеры алгоритмов оптимального управления режимами
|
|
В лекции рассмотрены: примеры алгоритмов оптимального управления технологическими режимами объектов; задачи и алгоритмы оптимального автоматизированного управления периодическими процессами, режимами пуска и остановка объекта; задачи оптимального управления дискретными технологическими процессами
Задачи и алгоритмы оптимального автоматизированного управления периодическими процессами. При автоматизации технологических объектов существенное место занимают задачи переключения оборудования по циклическим (временным) программам. Распространенность таких задач, как и приведенных ниже задач логического управления, обусловлена спецификой химического производства, в которой важная роль отводится аппаратам периодического действия.
В качестве алгоритма работы таких систем используются так называемые циклограммы – графики в координатах Y-X где по оси Y указывается исполнительные механизмы регулирующих органов, управляющие потоками рабочих веществ, Э/Д мешалок, транспортеров, задвижек и т.д., а по оси X –время их включения и отключения.
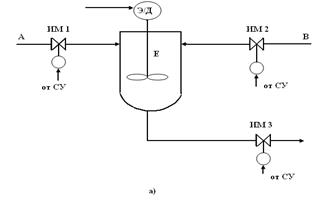
В качестве примера рассмотрим емкость E, в которую подаются компоненты A и B. После перемешивания потоков A и B (мешалка с Э/Д) осуществляется их слив. Схема объекта и циклограмма работы системы приведены на рисунке 5.1.
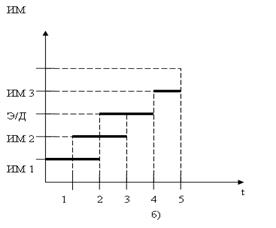
Из циклограммы видно, что поток А подается в емкость в течение первых 2-х минут. Поток B подается также в течение 2-х минут, начиная со второй минуты. Перемешивание включается, начиная с 3-й минуты, и длится тоже 2 минуты. По истечении четырех минут включается СЛИВ, который продолжается одну минуту.
Циклические системы относят к так называемым “безрефлексным” системам, т.к. они работают по жестким временным программам, независимо от состояния технологического объекта. Например, в приведенной на рисунке 13.1 системе перемешивание с помощью мешалки (Э/Д) включается независимо от того были поданы в емкость компоненты А и В при открытии клапанов ИМ.1 и ИМ.2 или нет.
Реализуются циклические системы, как правило, с помощью специальных устройств (программаторов) или контроллеров, запрограммированных на циклическое управление[1, 2].
| 
|
Рисунок 13.1 Технологический объект (а) и алгоритм работы (б) циклической системы управления (циклограмма)
Логическое управление и логические системы с памятью. Под логическим управлением подразумевается обеспечение при помощи автомата заданной логической связи между сигналами, поступающими от измерительных преобразователей, дающих информацию о состоянии объекта, и управляющими воздействиями на исполнительные устройства.
Любой автомат, как и всякая физическая система, характеризуется двумя факторами: схемой управления, которая в аналитическом виде может быть представлена системой уравнений алгебры логики, и способом реализации этой схемы, который в свою очередь, зависит от вида и конструкции используемых в автомате элементов (электронных, электромеханических, пневматических и других устройств релейного типа).
В соответствии с двумя указанными признаками автомата задача логического управления решается в 2 этапа:
1. Анализ работы объекта и составление алгоритма управления.
2. Синтез автомата, реализующего полученный алгоритм.
В качестве информации о процессе используются сигналы двух уровней, условно обозначаемых символами “0” и “1”. Два уровня сигнала соответствуют двум возможным состояниям параметра.
Таблица состояний. В общем случае состояние объекта в каждый момент времени характеризуется совокупностью дискретных (0 или 1) значений достаточного большого числа параметров и может быть представлено таблицей состояний (таблица 13.1).
Таблица 13.1
Таблица состояний
| х1 | х2 | х3 | … | хj | … | xN |
| … | … |
Каждая строка этой таблицы соответствует одному из возможных состояний объекта, для оценки свойств которого используется N параметров. В каждой строке фиксируется один из возможных наборов значений входных параметров x1, x2 , x3, , …, xN. Общее число возможных (с точки зрения переключательных операций) состояний объекта равно 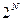 .
.
Таблицы включений. ри управлении процессом каждому набору значений входных сигналов ставятся в соответствие определенные дискретные значения выходных, или управляющих, сигналов y1, y2 , …, yN. Взаимосвязь входных и управляющих сигналов можно выразить при помощи так называемых таблиц включений, одна из которых для случая трех входных и одного выходного параметров приведена ниже (таблица 13.2).
Таблица 13.2
Таблицы включений
| х1 | х2 | х3 | у | х1 | х2 | х3 | у |
Зависимость между значениями входных и выходного сигналов, выраженная в этой таблице, характеризует определенную стратегию переключения, и поэтому ее можно рассматривать как алгоритм управления.
Приведенная таблица включения соответствует реализации некоторой логической зависимости общего вида y = f (x1, x2, x3), которую можно представить, воспользовавшись элементарными функциями алгебры логики. При этом принимается, что любая, сколь угодно сложная функция алгебры логики аналитически выражается через три элементарные операции: логическое сложение, логическое умножение и отрицание. Трем указанным элементарным функциям соответствуют следующие таблицы включения, в которых использованы обозначения в символах алгебры логики:
Логическое сложение (“ИЛИ”) … y = x1 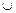 U x2 (таблица 5.3)
U x2 (таблица 5.3)
Логическое умножение (“И”) … y = x1 ∩ x2 (таблица 5.4)
Отрицание (“НЕ”) … y = 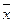 (таблица 5.5)
(таблица 5.5)
Любую сложную логическую зависимость можно представить как комбинацию элементарных функций алгебры логики
Использование таблиц включений в качестве исходного материала для составления алгоритма управления, выражаемого в терминах алгебры логики, не всегда оказывается возможным. Применение этих таблиц оправдано лишь тогда, когда зависимость между сигналами относительно проста. При большом числе независимых переменных указанный метод становится неудобным, так как составление таблиц связано с перебором всех возможных сочетаний значений аргументов. Например, при N =10 число строк таблицы включений составляет 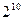 =1024. Кроме того, таблицы включения позволяют представить алгоритм управления лишь ограниченного класса логических автоматов, для которых характерна неизменность внутреннего состояния. В таких автоматах определенному набору значений входных аргументов x соответствуют строго определенные значения выходных функций y (рисунок 13.2).
=1024. Кроме того, таблицы включения позволяют представить алгоритм управления лишь ограниченного класса логических автоматов, для которых характерна неизменность внутреннего состояния. В таких автоматах определенному набору значений входных аргументов x соответствуют строго определенные значения выходных функций y (рисунок 13.2).
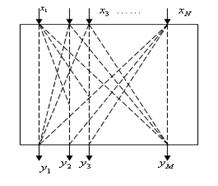
Рисунок 13.2 Выходные аргументы и входные переменные в логических автоматах
Системы управления с памятью. Большинство встречающихся на практике логических автоматов относится к категории систем управления с памятью, в которых набор выходных сигналов, вырабатываемых за некоторый отрезок времени, зависит не только от входных сигналов, поданных в тот же момент, но и от сигналов, поступивших ранее. Эти предшествующие внешние воздействия фиксируются в автомате путем изменения его внутреннего состояния. Реакция такого автомата определяется как поступившим набором входных сигналов, так и его внутренним состоянием в данный момент.
Характерной особенностью систем логического управления с памятью является наличие обратных связей в структуре автомата (рисунок 13.3).
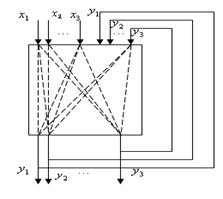
Рисунок 13.3.Обратные связи в структуре логического автомата
Существование обратных связей учитывается также в системе уравнений, соответствующей алгоритму управления системы с памятью:
y1 = f 1(x1, x2 , …, хN ; у1, у2 , …, уМ)
y2 = f2 (x1, x2 , …, хN ; у1, у2 , …, уМ)
y3 = f3 (x1, x2 , …, хN ; у1, у2 , …, уМ) (13.1)
………………………………….
yM = fM (x1, x2 , …, хN ; у1, у2 , …, уМ).
Отличительными признаками системы уравнений (13.1) является наличие в правой части символов y. Значения сигналов у1, у2 , …, уМ определяют «внутреннее» состояние автомата в момент изменения какого либо из входных сигналов 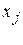 .
.
Ячейка памяти. Простейшим автоматом, реализующим алгоритм с обратной связью, является блок, содержащий элементарную ячейку памяти. Она осуществляет функцию запоминания на своем входе сигнала 1, поступившего на ее вход, после того, как там снова установиться сигнал 0.
Ячейке памяти соответствует уравнение вида y = x1 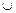 (x2 ·у)Рассмотрим возможные значения выходного параметра ячейки y в зависимости от входных сигналов x1 и x2.
(x2 ·у)Рассмотрим возможные значения выходного параметра ячейки y в зависимости от входных сигналов x1 и x2.
1. Пусть начальное значение состояния ячейки характеризуется соотношением сигналов x1 = 0 и x2 = 0. В этом случае y должен принять значение 0, что следует из уравнения y = 0 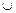 (0 · у), котороепревращается в тождество вида 0 · 0
(0 · у), котороепревращается в тождество вида 0 · 0 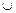 (0 · 0).
(0 · 0).
2.Пусть теперь при x1 = 0 сигнал x2 = 1; тогда уравнение ячейки запишется в виде y = 0 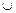 (1 · у).Пот такой ситуации y может принимать значения как 0 так и 1. Однако в момент поступления сигнала x2 = 1 параметр у = 0. Поэтому тождество примет вид 0 · 0
(1 · у).Пот такой ситуации y может принимать значения как 0 так и 1. Однако в момент поступления сигнала x2 = 1 параметр у = 0. Поэтому тождество примет вид 0 · 0 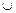 (1 · 0), и значение y = 0 сохраниться.
(1 · 0), и значение y = 0 сохраниться.
3. Пусть теперь x1 = 1 при условии x2 = 0. Тогда y = 1 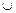 (1 · у).Правая часть уравнения должна обращаться в 1 при любом значении y. Следовательно, y= 1, и это уравнение превратиться в тождество вида 1 · 1
(1 · у).Правая часть уравнения должна обращаться в 1 при любом значении y. Следовательно, y= 1, и это уравнение превратиться в тождество вида 1 · 1 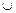 (1 · 1).
(1 · 1).
4. При условии y = 1и x2 = 1 снова установим x1 = 0. Тогда уравнение запишется в виде y = 0 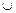 (1 · у). Поскольку y = 1, тождество должно принять вид 1 · 0
(1 · у). Поскольку y = 1, тождество должно принять вид 1 · 0 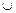 (1 · 1), при котором y =1 сохраняется. Таким образом, происходит «запоминание» y = 1 после того, как стало x1 = 0.
(1 · 1), при котором y =1 сохраняется. Таким образом, происходит «запоминание» y = 1 после того, как стало x1 = 0.
5. Для того чтобы теперь тут установить y = 0, необходимо обеспечить x2 = 0 при условии x1 = 0. Тогда уравнение ячейки примет вид y = 0 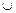 (0 · у), при котором восстановиться тождество 0 · 0
(0 · у), при котором восстановиться тождество 0 · 0 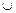 (0 · 0).
(0 · 0).
Из рассмотрения уравнения ячейки памяти следует, что между значениями входных параметров x1 и x2 и функций y нет жесткой связи, характерной для систем, не обладающих памятью.
Неоднозначность связей (см.п. 2 и 4) между параметрами обуславливает необходимость составления ряда таблиц включения для описания одной функции с обратной связью вида y = f (x1, x2, у). Построение алгоритмов управления систем с памятью на основе серии таблиц включения возможно лишь в немногих простейших случаях. Как правило, алгоритмы процессов переключения нужно сразу формулировать в терминах алгебры логики на основе анализа логических взаимодействий параметров и выбранной стратегии управления. Применение метода логического анализа при составлении алгоритма управления, вообще говоря, требует проведения довольно сложных рассуждений. Данный метод требует от составителя определенных навыков. Однако навыки приобретаются по мере решения практических задач, а сам метод логического анализа во многих случаях является единственным, позволяющим сформулировать алгоритм управлении и записать его в аналитической форме.
Логические преобразования. Этап алгоритмизации процесса переключения заканчивается получением аналитического описания в форме системы логических уравнений, аналогичных уравнениям вида (13.1). Однако для синтеза автомата по заданному алгоритму необходимо выполнить целый ряд логических преобразований, связанных с приведением системы уравнений к виду позволяющему затрачивать минимальное число физических элементов схемы управления для реализации заданной стратегии переключения.
Логические преобразования проводятся в соответствии с правилами, вытекающими из основных соотношений алгебры логики. Остановимся на рассмотрении некоторых из них.
1. Для функций логического сложения и умножения справедливы переместительный и сочетательный законы:
 . (13.2)
. (13.2)
Кроме того, для этих двух функций справедливы два распределительных закона:
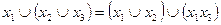 , (13.3)
, (13.3)
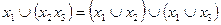 . (13.4)
. (13.4)
Формулы 13.2 и 13.3 имеют сходство с аналогичными формулами обычной алгебры, формула же 13.4 в обычной алгебре эквивалента не имеет.
2. Для функций алгебры логики справедливы также простые, но очень важные соотношения вида:
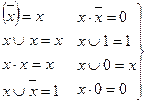 . (13.5)
. (13.5)
Таблица 13.3
Логическое преобразование х1 х2
| х1 | х2 | х1 х2 |
Таблица 13.4
Логическое преобразование 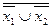
| х1 | х2 | 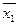
| 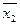
| 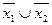
| 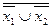
|
Таблица 13.5
Логическое преобразование х1 U х2
| х1 | х2 | х1 U х2 |
Таблица 13.6
Логическое преобразование 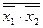
| х1 | х2 | 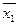
| 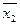
| 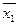 · · 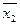
| 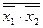
|
3. Кроме того, справедливы следующие основные формулы алгебры логики, которые чаще всего используются в логических преобразованиях:
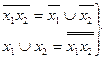 . (13.6)
. (13.6)
Справедливость соотношений (13.6) можно показать с помощью ряда таблиц приведенных выше таблиц 13.3 -13.6.
Следствиями формул (13.6) являются равенства (13.7)
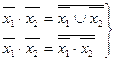 . (13.7)
. (13.7)
Синтез алгоритмов логического управления. Для определенности в качестве объектов управления возьмем группу контактных аппаратов (реакторов), работающих в режимах «контактирование – регенерация - контактирование» и решим задачу переключения этих аппаратов из одного режима в другой при следующих условиях:
1. В любой момент времени переключения необходимо производить так, чтобы обеспечивать постоянное число аппаратов, работающих в режиме контактирования.
2. При выходе очередного агрегата из режима регенерация на регенерацию переключается тот аппарат, который раньше других достиг своего оптимального времени контактирования 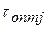 .
.
Последнее требование может служить критерием переключения.
Для более доступного изложения задачи введем некоторые упрощения. Допустим, что система управления должна обеспечивать оптимальную стратегию переключения для аппаратов, расположенных только в одной нитке. Для одной нитки в режим регенерации переводиться один аппарат. Остальные m -1 аппаратов в это время работают в режиме контактирования.
При указанном допущении предполагается, что для каждой нитки устанавливается автономная системная оптимального управления. Очевидно, что число таких систем, структура которых идентична, соответствует числу ниток.
Вывод контактных аппаратов на регенерацию будет осуществлять или по какому-либо технологическому критерию (например, степень контактирования G в аппарате, определяемая прибором качественного анализа), или экономическому критерию (среднесуточная норма прибыли R(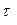 ), см. рисунок 13.4, рассчитываемая в специальном устройстве или ЭВМ).
), см. рисунок 13.4, рассчитываемая в специальном устройстве или ЭВМ).
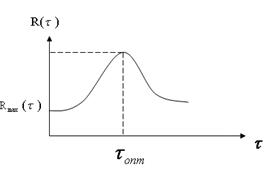
Рисунок 13.4. Функция средней прибыли: τ опт – оптимальное время переключения
При достижении функцией R(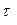 ) экстремального значения устройство выдает сигнал готовности к регенерации. Если к моменту поступления сигнала готовности предыдущий аппарат не успел выйти из режима регенерации, аппарат, от которого поступил сигнал готовности, становиться на очередь и в течение некоторого времени продолжает нести нагрузку.
) экстремального значения устройство выдает сигнал готовности к регенерации. Если к моменту поступления сигнала готовности предыдущий аппарат не успел выйти из режима регенерации, аппарат, от которого поступил сигнал готовности, становиться на очередь и в течение некоторого времени продолжает нести нагрузку.
Ацикличность процесса переключения, связанная с различием оптимального времени переключения 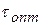 для отдельных аппаратов, может привести к возникновению ситуации, при которой несколько аппаратов один за другим подадут сигналы готовности к регенерации, в то время как один из аппаратов не закончил цикла регенерации. В этом случае аппараты должны встать на очередь в порядке поступления от них сигналов готовности аппаратов к регенерации.
для отдельных аппаратов, может привести к возникновению ситуации, при которой несколько аппаратов один за другим подадут сигналы готовности к регенерации, в то время как один из аппаратов не закончил цикла регенерации. В этом случае аппараты должны встать на очередь в порядке поступления от них сигналов готовности аппаратов к регенерации.
Как только закончится обработка аппарата, находящегося на регенерации, он подключается к нагрузке и на его место становится тот аппарат, который встал в очередь первым. К моменту вывода на регенерацию этот аппарат дальше других отойдет от своего оптимума, поэтому его дальнейшее использование в режиме контактирования наименее выгодно.
Установив критерий и стратегию переключения в форме словесного предписания, перейдем к составлению алгоритма управления, выраженного в терминах алгебры логики. Рассмотрение начнем с простейшего случая, когда в одной нитке имеются всего два аппарата, один из которых находиться в режиме контактирования, а другой в режиме регенерации.
Пусть х1 - сигнал от устройства расчета функции R(τ) для первого аппарата, а х2 - сигнал от аналогичного устройства для второго аппарата. Сигналы х1 и х2 принимают значения «0», если функции R1(τ) и R2(τ) не достигли своего экстремума. Соответственно х1 и х2 принимают значение «1» при переходе функций R1(τ) и R2(τ) через свои экстремальные значения. Значения сигналов х1 = 1 и х2 = 1 запоминаются до тех пор, пока соответствующий аппарат не пройдет стадию регенерации.
Пусть также у1 и у2 - сигналы, по которым дается разрешение на работу аппаратов в режиме регенерации. Сигнал у1 принимает значение «1», когда разрешается вывод на регенерацию первого аппарата. Второй аппарат также начинает работать в режиме регенерации при выполнении условия у2 = 1.
По условиям задачи параметр у1 может принимать значение «1» только при х1 = 1 (т.е. имеется сигнал готовности к регенерации первого аппарата). Соответственно у2 = 1 может быть только при условии х2 = 1.
Кроме того, должно удовлетвориться следующее требование. Если первый аппарат выводится на регенерацию раньше, чему соответствует у1 = 1, то второй аппарат блокируется, т.е. условие у2 = 0 должно соблюдаться до тех пор, пока первый аппарат не пройдет регенерацию. Данное логическое соотношение можно выразить уравнением
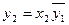 (13.8)
(13.8)
Аналогичные рассуждения для случая, когда раньше включается на регенерацию второй аппарат, приводят к выражению
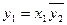 (13.9)
(13.9)
Система из двух полученных уравнений определяет алгоритм управления для двух аппаратов. Данный алгоритм реализует логическую систему с памятью, которая находиться в соответствии с принципом «кто раньше». Проверим найденный алгоритм, рассматривая различные сочетания значений аргументов:
1. Пусть первым пришел сигнал х1 = 1. Поскольку в предыдущий момент соблюдалось условие х2 = 0, то у2 =0, у1 = 0 обязательно. Следовательно, 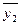 =1.
=1.
Поэтому в уравнении (10) получим: у1 =1·1=1. При таком сочетании сигналов первый аппарат включается на регенерацию.
2. Пусть теперь вслед за сигналом х1 = 1 пришел сигнал х2 = 1. Эта ситуация соответствует случаю, когда второй аппарат готов к регенерации, а первый аппарат еще не прошел стадию регенерации. Тогда у1 = 1, а 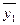 = 0. Следовательно, у2 =1·0=0. Второй аппарат не может быть включен на регенерацию до тех пор, пока ее не пройдет первый аппарат.
= 0. Следовательно, у2 =1·0=0. Второй аппарат не может быть включен на регенерацию до тех пор, пока ее не пройдет первый аппарат.
3. Когда первый аппарат закончит работу в режиме регенерации, сигнал х1 снова станет равным «0». Последует у1 =0· 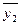 =0, откуда
=0, откуда 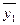 =1. Поскольку сигнал х2 =1 сохраняется, то у2 =1·1=1 и второй аппарат включается на регенерацию.
=1. Поскольку сигнал х2 =1 сохраняется, то у2 =1·1=1 и второй аппарат включается на регенерацию.
4. Если теперь поступит сигнал х1 = 1, в то время как второй аппарат не прошел регенерацию, первый аппарат встанет в очередь. Это следует из того, что 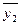 =1 и у2 =0. Отсюда у1 = 1·0=0 при х1 =1. Следовательно, первый аппарат встал в очередь.
=1 и у2 =0. Отсюда у1 = 1·0=0 при х1 =1. Следовательно, первый аппарат встал в очередь.
Перейдем теперь к рассмотрению общего случая, когда в одной нитке имеется m аппаратов, один из которых в каждый момент времени находиться на регенерации. Из работающих m аппаратов первым может подать сигнал готовности любой аппарат, например j -й. По условиям задачи сигнал у1 должен заблокировать, т.е. запретить включение на регенерацию всех остальных m -1 аппаратов. Для осуществления этого требования сигнал у1 должен быть связан логическим соотношением «кто раньше» с сигналами включения у всех остальных m -1 аппаратов. Следовательно, j -го аппарата связи сигналов с сигналами от других аппаратов выразятся следующими уравнениями:
С первым аппаратом
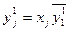 ,
, 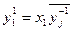 (1310)
(1310)
Со вторым аппаратом
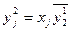 ,
, 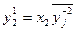 (13.11)
(13.11)
С m -м аппаратом
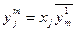 ,
, 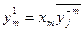 (13.12)
(13.12)
В этих уравнениях для параметра у введен дополнительный верхний индекс. Он указывает номер аппарата, с которым осуществляется связь «кто раньше». Нижний индекс, как и в простейшем случае для двух аппаратов, показывает номер аппарата, на который подается данный управляющий сигнал.
Из рассмотрения уравнения связи j -го аппарата следует:
1. Параметр yj может принимать значения «1», если j -й аппарат подает сигнал готовности к регенерации раньше, чем первый аппарат. Это значит, что в момент поступления сигнала xj =1 будет иметь место сигнал xj =0, тогда

Значит
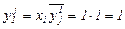
2. Параметр 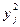 может принимать значение «1», если j -й аппарат подает сигнал готовности к регенерации раньше, чем второй аппарат. По аналогии с предыдущим можно утверждать, что
может принимать значение «1», если j -й аппарат подает сигнал готовности к регенерации раньше, чем второй аппарат. По аналогии с предыдущим можно утверждать, что 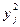 =1 и
=1 и 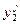 =0 и т.д.
=0 и т.д.
Параметр 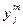 может принять значение «1», если j -й аппарат подает сигнал готовности к регенерации раньше, чем m -й аппарат. В этом случае
может принять значение «1», если j -й аппарат подает сигнал готовности к регенерации раньше, чем m -й аппарат. В этом случае 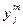 =1 и
=1 и 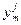 =0.
=0.
По условиям задачи для включения j -го аппарата на регенерацию необходимо, чтобы сигнал готовности пришел от него раньше всех остальных сигналов, т.е. чтобы все значения 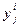 , где i =1, 2, 3, … j -1, j +1, … m, были равны 1. Если же хотя бы один из сигналов, например от j -го аппарата, поступит раньше, чем сигнал от j -го аппарата, то j -й аппарат должен не включаться, а встать в очередь за l-м аппаратом. Такой ситуации соответствует значение
, где i =1, 2, 3, … j -1, j +1, … m, были равны 1. Если же хотя бы один из сигналов, например от j -го аппарата, поступит раньше, чем сигнал от j -го аппарата, то j -й аппарат должен не включаться, а встать в очередь за l-м аппаратом. Такой ситуации соответствует значение 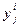 =0, в то время как
=0, в то время как 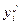 =1.
=1.
Обозначим через 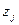 выходной управляющий параметр для j -го аппарата. Согласно изложенной стратегии переключений связь с параметрами
выходной управляющий параметр для j -го аппарата. Согласно изложенной стратегии переключений связь с параметрами 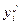 (где i = 1, 2, 3, …,
(где i = 1, 2, 3, …, 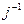 ,
, 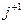 , …, m) можно представить следующим логическим соотношением:
, …, m) можно представить следующим логическим соотношением:
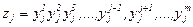
В самом деле 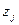 =1 только в том случае, когда все значения
=1 только в том случае, когда все значения 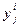 , где i = 1, 2, 3, …, j -1, j +1, …, m, равны «1». Если же хотя бы одно из значений
, где i = 1, 2, 3, …, j -1, j +1, …, m, равны «1». Если же хотя бы одно из значений 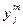 равно «0», то
равно «0», то 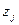 также обращается в 0.
также обращается в 0.
Совершенно очевидно, что, поскольку индекс j может принимать любые значения (j =1, 2, 3, …, m -1, m), для управляющих сигналов всех 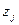 аппаратов получим систему уравнений вида:
аппаратов получим систему уравнений вида:
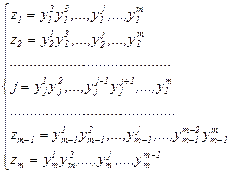 (13.13)
(13.13)
В данной системе уравнений все параметры y связаны между собой соотношениями вида
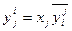
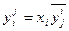 ,
,
которые мы будем называть уравнениями связи.
Определим теперь общее число уравнений связи для случая m аппаратов. На каждые два аппарата из числа m приходиться по два уравнения связи.
Если число возможных пар из числа m равно числу сочетаний из m по 2, т.е. 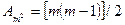 , то общее число уравнений связи составляет:
, то общее число уравнений связи составляет:
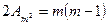 (13.14)
(13.14)
Полученный в аналитическом виде алгоритм управления можно представить в форме структурной схемы, показанной на рисунке 5.5 для случая m = 3.
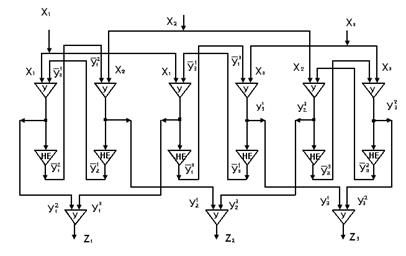
Рисунок 13.5. Структурная схема алгоритма управления тремя аппаратами