Для нахождения моделей тренда

Наименование функции	Вид функции	Система нормальных уравнений
Линейная
Парабола второго порядка
Парабола третьего порядка
Показательная
Гиперболическая

Рассмотрим выравнивание рядов динамики по линейной функции и методы определения ее параметров.

Выравнивание по линейной функции .

Метод наименьших квадратов дает систему нормальных уравнений для нахождения параметров и :

где 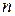- количество уровней ряда;

- исходный уровень ряда динамики;

- показатель времени, который обозначается порядковыми номерами, начиная от низшего.

Решение системы уравнений имеет вид:

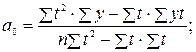
Cистема нормальных уравнений и расчет параметров и упрощается, если отсчет времени вести от середины ряда. Показателям времени придаются такие значения, чтобы их сумма была равна нулю, т.е.

§ при нечетном числе уровней ряда n, срединная точка принимается за нуль. Тогда периоды времени обозначаются так:

§ при четном числе уровней ряда n, два срединных момента (периода) обозначают -1 и +1, а все предыдущие и последующие, соответственно, через два интервала: .

При таком подходе каждое из уравнений системы решается самостоятельно:

При этом значение параметра представляет собой средний уровень ряда динамики .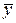

По полученной модели тренда для каждого периода (каждой даты) определяются теоретические уровни тренда . Также рассчитывается среднее квадратическое отклонение тренда (стандартная ошибка аппроксимации):

,

где n – число уровней ряда;

m – число параметров в уравнении тренда;

, - соответственно фактические и расчетные (выровненные) значения уровней ряда.

Значение ошибки тренда находят для получения наиболее подходящей кривой. Относительной мерой колеблемости является коэффициент вариации, который вычисляется по формуле:

.

По окончании расчета основной тенденции рекомендуется построить график, на котором следует изобразить фактические и выровненные значения уровней ряда.

Выравнивание рядов динамики по другим функциям (парабола второго порядка, показательная функция и др.) выходит за рамки данного пособия, и подробно рассмотрено в учебниках по курсу общей теории статистики.

Следует заметить, что выравнивание по аналитическим формулам может быть использовано при прогнозировании (см. § 8.7) отдельных показателей путем экстраполяции ряда (нахождение уровней за пределами ряда).