Аналитическое описание переходного процесса 3-х фазного к.з. в простейшей эл.цепи при питании ее от источника неограниченной мощности.

СТРАНИЦА 58 УЧЕБНИКА

Симметричную трехфазную цепь с сосредоточенными активными со-

противлениями и индуктивностями, при отсутствии в цепи трансформатор-

ных связей, принято называть простейшей трехфазной цепью. Ее питание осуще­ствляется от источника, собственное сопротивление кото­рого равно нулю и его напряжение, изменяясь с постоян­ной частотой, имеет неизменную амплитуду. Обычно его называют источником бесконечной мощности

Известно, для любого момента времени для электрической цепи, содержаще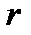й и 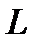, дифференциальное уравнение равновесия падений напряжений для любой фазы, например, для фазы 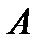, имеет вид

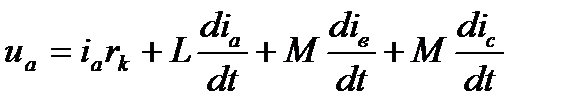, (3.1)

где 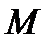-коэффициент взаимоиндукции между фазами.

Имея в виду, что в трехфазной сети с изолированной нейтралью в любой момент времени имеет место соотношение 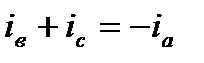, можно это уравнение представить (опуская индекс фазы)

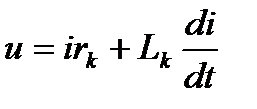, (3.2)

где - результирующая индуктивность фазы, то есть индуктивность с учетом влияния двух других фаз.

Решение (3.2), например, для фазы , имеет вид (для дифференциального уравнения первого порядка с правой частью, отличной от нуля)

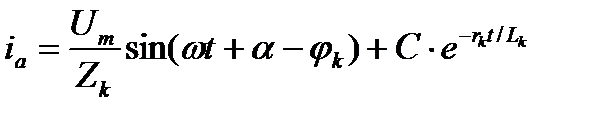, (3.3)

где 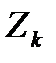- полное сопротивление присоединенного к источнику участка цепи или цепи к.з.; - угол, определяющий значение проекции 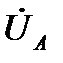на ось времени в момент времени 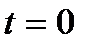(иначе, фаза включения);

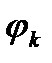- угол сдвига тока фазы по отношению к напряжению фазы в цепи к.з.;

- постоянная времени цепи к.з.

Первый член правой части (3.3) представляет собой синусоиду (периодическую слагающую полного тока 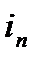), которая при рассматриваемых условиях является принужденным током с постоянной амплитудой 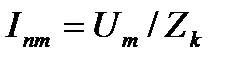. Соответственно, второй член решения представляет собой затухающий по закону экспоненты свободный ток (апериодическая слагающая полного тока), начальное значение которого определяют из начальных условий, то есть: .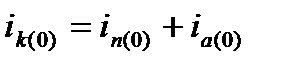

Согласно правилу Ленца в момент времени для фазы 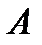, должен равняться току режима, предшествующему к.з.

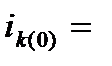
. (3.5)

Подставляя выражение 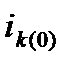из (3.5) в (3.4), получим

, (3.6)

где 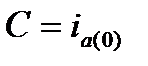- начальное значение апериодической слагающей тока к.з.

Следовательно, можно записать

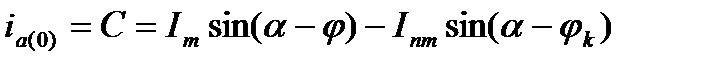. (3.7)

Переходя к обозначениям, принятым в расчетах токов к.з, можно записать, что для любой фазы ,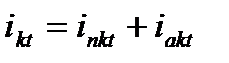

где 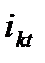- мгновенное значение полного тока к.з.; 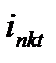- мгновенное значение периодической слагающей полного тока к.з.; 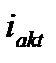- мгновенное значение апериодической слагающей полного тока к.з.

Подставляя значения 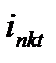и 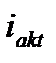из (3.3) и (3.7), можно для фазы 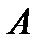записать

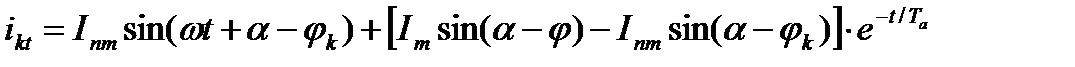. (3.8)

Выражение (3.8) определяет полный ток фазы 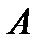при трехфазном к.з. в переходном процессе (при питании короткозамкнутой цепи от источника неограниченной мощности).

Следовательно, значение 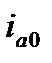можно представить как 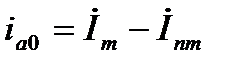или

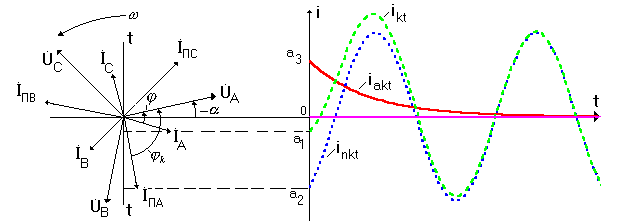
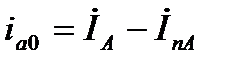, то есть как разность векторов 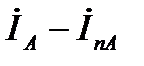, спроектированную на ось времени (см. рис.3.3).

Рис.3.3.

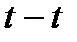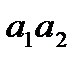Отмечая на оси значения проекции этой разности, получаем в виде отрезка . Там же (на оси отрезки 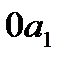-мгновенное значение полного тока до к.з., а -мгновенное значение периодической слагающей тока к.з.

На оси 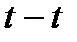откладываем начальное значение апериодической слагающей тока к.з. 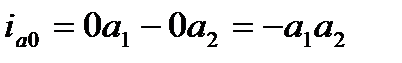. Поэтому отрезок 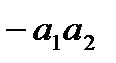отложен вверх от точки 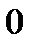по оси (отрезок ).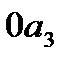

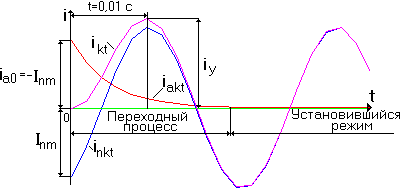
Развертывая далее переходный процесс во времени, получим осциллограмму рис.3.3.

На осциллограмме отмечены: 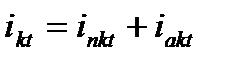-полный ток к.з. (для фазы );

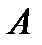-периодическая слагающая тока к.з.; -апериодическая слагающая тока к.з.

6.Порядок расчета ударного и действующего токов к.з. при 3-х фазном к.з. в простейшей трехфазной цепи.

Ударный ток короткого замыкания

Под ударным током к.з. 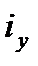понимают наибольшее мгновенное значение полного тока к.з. в фазе через 0, 01 с после возникновения к.з. (см. рис.3.5).

или, если взять нижние знаки

, (3.12)

где .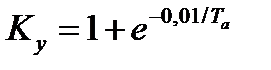

называют ударным коэффициентом. Он показывает во сколько раз ударный ток к.з. больше начальной амплитуды периодической слагающей тока к.з.

Если принять 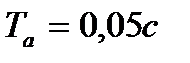, то .

Рассмотрим возможные пределы изменения для электрической цепи с активно-индуктивным характером.

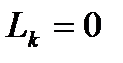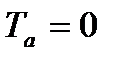1) Если то , следовательно,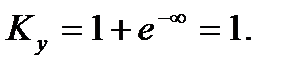

2) Если то , следовательно,

Таким образом, величина ударного коэффициента может находится в пределах .

Действующее значение тока короткого замыкания

Под действующим значением полного тока к.з. понимают среднеквадратичный ток к.з. за период, в центре которого расположен рассматриваемый момент времени. Значение этого тока определяют по выражению

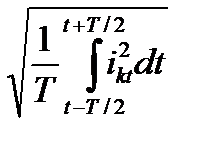. (3.14)

Если в (3.14) значение выразить через его составляющие 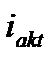, и произвести соответствующие преобразования [1], то получим

, (3.15)

где - действующее значение периодической слагающей тока к.з.;

действующее значение апериодической слагающей тока к.з. в момент времени .

Наибольший практический интерес представляет действующее значение тока к.з. в течение первого периода к.з., то есть в том периоде времени, в котором расположен ударный ток к.з. В этом случае действующее значение тока к.з. принято обозначать .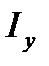

Согласно формуле (3.15) можно записать

,

где (так как цепь к.з. подключена к источнику неограниченной мощности); .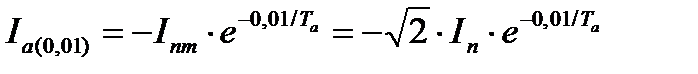

Тогда 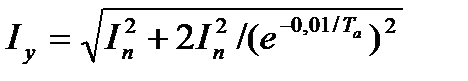или окончательно,

. (3.17)

Имея в виду, что может изменяться от 1 до 2, получим, что по выражению (3.17) может находиться в пределах

.
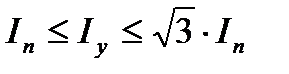