
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Турнирная сортировка
|
|
Бинарные деревья находят применение в качестве деревьев принятия решений. Например, при представлении спортивного турнира, где каждый внутренний узел соответствует победителю встречи между двумя игроками.
Турнирное дерево может использоваться для сортировки массива из n элементов.
Рассмотрим алгоритм турнирной сортировки на следующем примере:
Пусть имеется массив из 8-ми элементов A [8]={35, 25, 50, 20, 15, 45, 10, 40}. Необходимо его отсортировать по возрастанию.
1. Элементы массива запоминаются в бинарном дереве на уровне k, где  ; n – это количество элементов массива.
; n – это количество элементов массива.
В данном случае элементы массива А запоминаются на уровне 3 ( ).
).

2. В родительские узлы помещаются наименьшие значения в парах. В результате последнего сравнения наименьший элемент массива попадает в корень дерева на уровне 0.

3. Наименьший элемент удаляется со своего старого места на дереве и копируется во вспомогательный массив.

Так как один элемент был удален, то п.2 выполняется заново, но уже без удаленного элемента.

4. Аналогичные действия выполняются с числом 15:

5. Процесс продолжается до тех пор, пока все листья не будут удалены. Последний (наибольший) узел играет серию матчей, в которых побеждает всех по умолчанию:


Вычислительная эффективность
Эффективность турнирной сортировки составляет  .
.
В массиве, содержащем n = 2 k элементов, для выявления наименьшего элемента требуется n -1 сравнений.
Общее число матчей равно
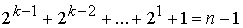 .
.
Дерево обновляется, и оставшиеся n -1 элементов обрабатываются посредством k -1 сравнений вдоль пути, проходящего через родительские узлы.
Общее число сравнений равно
 .
.