Пирамиды (heap - tree)

Пирамида - законченное бинарное дерево, имеющее упорядочение узлов по уровням.

Различают максимальные пирамиды и минимальные.

В максимальной пирамиде родительский узел больше или равен каждому из своих сыновей. Корень содержит наибольший элемент.

В минимальной пирамиде родительский узел меньше или равен каждому из своих сыновей. Корень содержит наименьший элемент.

Пирамида используется в тех приложениях, где клиенту требуется прямой доступ к минимальному элементу.

Пирамида является списком, который хранит данные в виде бинарного дерева.

Все алгоритмы обработки пирамид сами должны обновлять дерево и поддерживать пирамидальное упорядочение.

Преобразование массива в пирамиду

Индекс последнего элемента пирамиды равен n -1.

Индекс его родителя равен (n -2)/2, и он определяет последний нелистовой узел пирамиды. Этот индекс является начальным для преобразования массива.

Рассмотрим целочисленный массив

int A[10] = {9, 12, 17, 30, 50, 20, 60, 65, 4, 19}; Индексы листьев: 5, 6,..., 9. Индексы родительских узлов: 4, 3,..., 0.
Родитель А [4]=50, он больше своего сына А [9]=19 и поэтому должен поменяться с ним местами.
Родитель А [3]=30, он больше своего сына А [8]=4 и поэтому должен поменяться с ним местами (если меньших сына два, то меняется местами с наименьшим сыном).
На уровне 2 родитель А [2]=17 уже удовлетворяет условию пирамидальности, поэтому перестановок не производится. Родитель А [1]=12 больше своего сына А [3]=4 и должен поменяться с ним местами.
Процесс прекращается в корневом узле. Родитель А [0]=9 должен поменяться местами со своим сыном А [1]. Результирующее дерево является пирамидой.

Включение элемента в пирамиду

1. Новый элемент добавляется в конец списка.
2. Если новый элемент имеет значение, меньшее, чем у его родителя, узлы меняются местами.
3. Новый родитель рассматривается как сын, и проверяется условие пирамидальности для более старшего родителя.
4. Процесс сканирует путь предков и завершается, встретив родителя, меньше чем новый элемент, или достигнув корневого узла.

Удаление из пирамиды

Данные удаляются всегда из корня дерева.

1. Удалить корневой узел и заменить его последним узлом.
2. Если новый корневой узел больше любого своего сына, то необходимо его поменять местами с наименьшим сыном.
3. Движение по пути меньших сыновей продолжается до тех пор, пока элемент не займет правильную позицию в качестве родителя или пока не будет достигнут конец списка.

Пирамидальная сортировка

1. Преобразовать массив в пирамиду.

2. Последовательное исключение A [0] и включение его в A [ n -1], A [ n -2],..., A [1]. (Этот алгоритм основан на том, что после исключения элемента из пирамиды элемент, бывший до этого хвостовым, замещает корневой узел, а его место освобождается.

В процессе пирамидальной сортировки очередные наименьшие элементы удаляются и последовательно запоминаются в хвостовой части массива. Таким образом производится сортировка по убыванию.

Пример:

Дан массив: int A[]={50, 20, 75, 35, 25}; Исходная пирамида
Удалить 20 и запомнить в A [4]	Удалить 25 и запомнить в A [3]
Удалить 35 и запомнить в A [2]	Удалить 50 и запомнить в A [1]

Поскольку остался только корень, то массив отсортирован: А = 75, 50, 35, 25, 20.

Вычислительная эффективность

Массив, содержащий n элементов соответствует законченному бинарному дереву глубиной .

Преобразование массива в пирамиду требует n /2 операций, каждая из которых требует не более k сравнений.

Вторая фаза сортировки требует выполнения n -1 операции, которая в худшем случае требует k сравнений.

Худший случай сложности пирамидальной сортировки

.

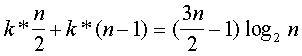Сложность алгоритма имеет порядок .

Пирамидальная сортировка не требует дополнительной памяти (для сравнения: при турнирной сортировке требуется создание дополнительного массива).

3.5. Сбалансированные деревья