
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Б-деревья
|
|
Важная область применения сильноветвящихся деревьев - формирование и использование крупномасштабных деревьев поиска, которые хранятся не в оперативной памяти, а на внешнем запоминающем устройстве (например, на диске).
В отличие от деревьев в оперативной памяти, в данном случае ссылки представляют собой не адреса оперативной памяти, а адреса на диске (номера записи в файле).
Сильноветвящиеся деревья позволяют организовать память таким образом, что требуется наименьшее число обращений к диску за счет того, что можно обратиться сразу к группе элементов дерева.
Структурно это можно представить следующим образом:

Дерево разделено на поддеревья, называемые страницами (в данном случае на каждой странице 7 узлов).
Однако при организации сильноветвящихся деревьев необходима схема управления их ростом.
Разумный критерий был сформулирован Р.Бэйером для структур данных, называемых Б-деревьями:
1. Каждая страниц содержит не более 2 n элементов (n - порядок Б-дерева).
2. Каждая страница, кроме корневой, содержит не менее n элементов.
3. Каждая страница является либо листом, т.е. не имеет потомков, либо имеет m +1 потомков, где m - число находящихся на ней ключей.
4. Все листья находятся на одном и том же уровне.
Б-дерево второго порядка с тремя уровнями:
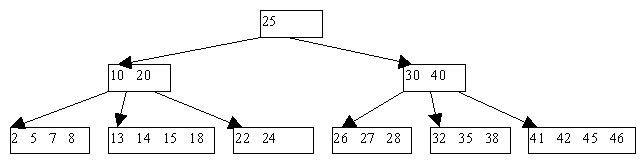
· Все страницы содержат 2, 3, 4 элемента.
· Корню разрешается иметь только один элемент.
· Все листья находятся на уровне 3.
· Ключи расположены в возрастающем порядке слева направо.
· Если потомков вставить между ключами на странице-предке, то порядок не нарушится.
Поиск по Б-дереву
Пусть задан аргумент поиска х.
Предположим, что оперативную память считана какая-то страница Б-дерева

где  - ключи;
- ключи; 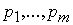 - указатели на страницы-потомки.
- указатели на страницы-потомки.
Если m достаточно велико, то можно применить бинарный поиск, если оно небольшое, то можно применить и последовательный поиск.
Возможны следующие ситуации:
1. x = =  , искомый элемент найден.
, искомый элемент найден.
2. 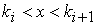 для 1 £ i < m. Продолжаем поиск на странице
для 1 £ i < m. Продолжаем поиск на странице  .
.
3.  . Продолжаем поиск на странице
. Продолжаем поиск на странице 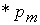 .
.
4. 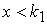 . Продолжаем поиск на странице
. Продолжаем поиск на странице  .
.
5. Если ссылка равна NULL, то элемента с таким ключом нет во всем дереве.
Для представления Б-дерева в оперативной памяти можно выбрать следующую структуру:
typedef struct page {
int m; //количество элементов на данной странице
//n< =m< =nn
page *p0; //указатель на левую страницу-наследник
struct { //элементы страницы (в виде массива)
int key;
page *p;
}item[nn]; //nn - максимальное количество элементов
//на странице nn=2n
};
Включение в Б-дерево
Возможны две ситуации:
1. Элемент вставляется в страницу, содержащую m < 2n элементов. Тогда процесс включения ограничивается данной страницей.
2. Включение элемента в заполненную страницу:
a) поиск по дереву элемента с данным ключом, и если такого элемента нет, то определение страницы, где элемент должен быть;
b) если на этой странице количество элементов m < 2 n, то включение производится только на данной странице;
c) иначе размещается новая страница, количество ключей m +1 (ключ, который вставляется) поровну распределяется на две страницы, а средний ключ перемещается на уровень вверх;
d) все выполняется, начиная с пункта d но уже со страницей верхнего уровня.
В экстремальном случае расщепление может распространиться до корня. Следовательно, Б-дерево растет от листьев к корню.
Рассмотрим на примере:
Необходимо включить ключ 22 в Б-дерево порядка 2.
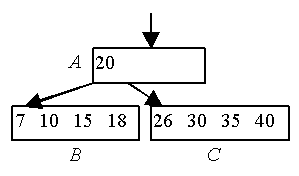
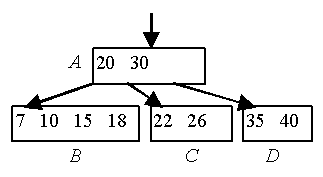
1. Выяснить, что ключ 22 отсутствует. Включение в страницу С невозможно, т.к. она заполнена.
2. Страница С расщепляется на две страницы (С и D).
3. Элементы страницы С + 1 поровну распределяются на страницы C и D, а средний элемент перемещается на уровень выше на страницу-предок А.
· Можно функцию поиска с включением описать рекурсивно.
· Каждое обращение к данной функции предполагает размещение в оперативной памяти всего одной страницы.
· Максимум необходимо 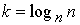 рекурсивных обращений.
рекурсивных обращений.
Вывод: если дерево содержит т элементов, то мы должны иметь возможность разместить в оперативной памяти k страниц (именно это накладывает ограничения на размер страницы).
Удаление элементов из Б-дерева
Возможны два случая:
1. Удаляемый элемент находится на странице-листе. Тогда алгоритм прост и очевиден.
2. Удаляемый элемент находится не на странице-листе.
Алгоритм
1. Производим поиск смежного ключа (самый правый левого поддерева или самый левый правого поддерева). Допустим, находим его на странице Р.
2. Заменяем удаляемый элемент на смежный, а Р уменьшаем на единицу.
3. Проверяем число элементов на уменьшенной странице Р. Если m < n, то нарушено свойство Б-деревьев и нужно совершить дополнительные действия:
· балансировку: в оперативную память вызывается одна из соседних страниц Q; элементы страниц P и Q поровну распределяются на обе страницы.
· слияние: используется, если страница Q достигла своего минимального значения. Процесс слияния полностью обратен процессу расщепления, общее число элементов на страницах P и Q равно 2 n -1; можно слить эти страницы в одну и добавить средний элемент со страницы предка P и Q.
· удаление среднего ключа на странице-предке может также уменьшить ее размер ниже допустимой границы, тогда требуются балансировка или слияние на более высоком уровне. (В экстремальном случае слияние страниц распространяется до корня, что может вызвать уменьшение высоты Б-дерева).