Частотные методы

Динамические свойства объекта могут быть описаны с помощью частотных характеристик. Частотная характеристика объекта представляет зависимость от частоты в установившемся режиме двух переменных:

1) Отношения амплитуд гармонических сигналов на входе и выходе объекта – амплитудно-частотная характеристика (АЧХ) А(ω);

2) сдвига фаз между входными и выходными гармоническими сигналами – фазочастотная характеристика (ФЧХ) φ (ω).

На графиках принято изображать указанные характеристики в следующих формах.

1. В виде совокупности АЧХ и ФЧХ в декартовых координатах в зависимости от частоты. Эта форма графика называется диаграммой Боде.

2. В полярных координатах, где А(ω) является радиусом-вектором, φ (ω) – полярным углом. Частота ω является параметром. Такая кривая с отметками частот носит название амплитудно-фазовой характеристики (АФХ) или диаграммы Найквист а.

Принято также использовать известную форму записи функций, заданных в полярных координатах, в виде комплексных чисел. Действительная часть W(jω) записывается в виде

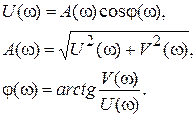
- мнимая частотная характеристика, - вещественная частотная характеристика.

Мнимая – в виде

Амплитудно-фазовая характеристика в символической записи имеет вид:

3. Если в диаграммах Боде А(ω) заменены на lgА(ω), то характеристики носят название логарифмических частотных характеристик. При этом обычно по оси абсцисс откладывается относительная частота в логарифмическом масштабе в октавах и декадах, а по оси ординат вместо lgА откладывается 20 lgА в децибелах.

Выражения W(jω), А(ω), φ (ω), , могут быть легко найдены, если известно дифференциальное уравнение. Для этого достаточно в выражении подставить jω вместо р. Полученное комплексное число и представляет собой аналитическое выражение АФХ в комплексной форме W(jω). Остальные формы характеристик могут быть легко получены по известным правилам преобразования комплексных чисел. Заданные аналитически или графически частотные характеристики объекта позволяют рассчитать контур стабилизации со стандартным регулятором.

Рис.2.3. Схема определения частотных характеристик в замкнутой системе

Эксперимент, с помощью которого исследуются частотные характеристики, значительно более трудоемок по аппаратуре и времени проведения по сравнению с переходными характеристиками. Для исследования необходима аппаратура, с помощью которой можно подать на вход объекта гармонические сигналы. Выходной сигнал всегда зашумлен и обычно несколько искажен нелинейностями, имеющимися в объекте. Поэтому для определения амплитуды и фазы выходного гармонического сигнала необходимо выделение первой гармонической составляющей вручную или с помощью специальной аппаратуры. Исследование на различных, в том числе низких частотах, требует большого времени.

Поскольку при исследовании частотных характеристик рассматривается вынужденное, а не свободное движение системы, необходимо некоторое время для затухания свободного движения.

На исследование частотных неблагоприятное влияние оказывают тренды, вызывающие «уползание» средней линии выходного сигнала. Для уменьшения ошибок из-за «уползания» средней линии и уменьшения влияния помех определение частотных характеристик производят в замкнутой системе по схеме, приведенной на рис.2.3, где объект с передаточной функцией W(p) охвачен обратной связью с регулятором-стабилизатором, имеющим передаточную функцию W_р(p). Помехи, приведенные к выходу объекта ξ (t), могут содержать кроме случайных составляющих детерминированные тренды. Но в сигнале y(t) «уползание» будет устранено, а воздействие случайных составляющих ξ (t) значительно ослаблено. Гармонический сигнал теперь будет подаваться с генератора Г не непосредственно на регулирующий орган, а на задатчик регулятора, что, конечно, требует значительно меньшей мощности генератора. На анализатор А, выделяющий первые гармонические составляющие, подаются сигналы x и y.

Полученные экспериментально частотные характеристики, как упоминалось выше, могут быть использованы для расчета системы управления. Однако более универсальным для различных применений является аналитическое представление.

Разработаны методы аппроксимации частотных характеристик аналитическими выражениями.