Вычисление коэффициентов модели

Приведем метод вычисления коэффициентов линейной модели с нормированными факторами

(6.23)

по результатам ПФЭ типа .

Используем матричный метод регрессионного анализа, который очень удобен для решения задач на ЭВМ. Для этого введем следующие матрицы:

матрицу независимых переменных

, (6.24)

матрицу — столбец откликов (вектор наблюдений) и матрицу — столбец коэффициентов

, (6.25)

и матрицу, транспонированную к

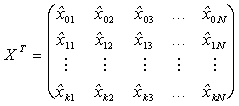. (6.26)

В матричной форме система нормированных уравнений для определения коэффициентов методом наименьших квадратов запишется следующим образом:

. (6.27)

Отсюда

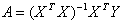. (6.28)

Матрица моментов (информационная матрица Фишера) 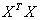имеет вид

, (6.29)

где суммирование всюду осуществляется по от 1 до .

Учитывая свойства ортогональности (6.20) матрица коэффициентов нормальных уравнений 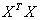становится диагональной и ее диагональные элементы равны

. (6.30)

Матрица, обратная матрица моментов , получается равной

. (6.31)

Далее имеем:

; (6.32)

, (6.33)

где суммирование осуществляется по от 1 до .

Следовательно, любой коэффициент определяется по формуле

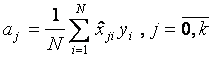. (6.34)

Если в рассмотрение ввести нелинейную модель с коэффициентами взаимодействия

, (6.35)

то эффекты взаимодействия определяются аналогично линейным эффектам:

; (6.36)

. (6.37)

и т.д.

В связи с тем, что матрица для спланированного эксперимента — матрица диагональная коэффициенты уравнения регрессии некоррелированы между собой. При этом выборочные коэффициенты оказываются несмешанными оценками для соответствующих генеральных коэффициентов , то есть величины коэффициентов уравнения регрессии характеризуют вклад каждого фактора в величину .

Если выход объекта зависит еще и от квадрата факторов

, (6.38)

то эксперимент типа не позволяет определить квадратичные эффекты . Действительно, значения не отличаются друг от друга и от вектор столбца 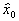. Поэтому величина представляет собой смешанную оценку значения свободного члена и вкладов квадратичных членов, то есть

,

где — вычисленный выше коэффициент;

— неизвестные истинные значения .

Для получения модели типа (6.38), включающей степени факторов, необходимо проводить эксперимент при .