Пример выполнения работы. Задача 2.1. Методом половинного деления найти корень уравнения с точностью e=0,01.

Задача 2.1. Методом половинного деления найти корень уравнения с точностью e=0, 01.

Решение:

Один из искомых корней принадлежит отрезку . На каждом шаге вычислений значение корня принимаем равным с погрешностью . Будем производить вычисления и выбирать последовательность вложенных отрезков , используя условие . Имеем

Так как 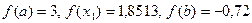и , то принимаем:

Тогда

Здесь

Следовательно,

Тогда

Производя вычисления, можно убедиться, что требуемая точность достигается на 7-м шаге: с погрешностью

Задача 2.2. Решить уравнение методом итераций с точностью .

Решение: Для отделения корней представим данное уравнение в виде . Построив графики функций и , увидим, что корень уравнения содержится внутри отрезка .

Здесь

Запишем уравнение в виде , где

Положим . Последовательные приближения найдём по формулам

.

Для оценки погрешности четвёртого приближения воспользуемся неравенством 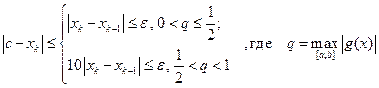. Так как , то . Следовательно, с точностью . Заметим, что мы получили приближённое значение корня с точностью более высокой, чем задано в условии.

Задача 2.3. Один из корней уравнения заключён в отрезке . Найти приближённое значение этого корня методом касательных с помощью двух итераций и оценить погрешность вычисления.

Решение. Здесь . Заметим, что на отрезке сохраняют знак и первая и вторая производные: . Таким образом, выполняются условия применения метода касательных. В качестве можно взять, например, 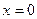, так как и . Тогда имеем . Оценим погрешность вычисления. Найдём значения необходимых параметров: .

Тогда .

Вторая итерация: .

Оценим погрешность вычисления: .

Таким образом, мы уже на второй итерации получили приближённое значение корня такой же точности, как в примере из предыдущей лекции лишь на седьмом шаге.

ПРАКТИЧЕСКАЯ РАБОТА №3

ТЕМА: «МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ»

Задание: