
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Математико – статистическая обработка результатов параллельных определений
|
|
Проведя серию аналитических определений того или иного компонента пробы (не менее 5 параллельных определений), прежде всего необходимо выявить те из полученных результатов, которые следует признать грубо ошибочными (промахами). Для этого при объеме выборки 5  10, как правило, используют так называемый Q–тест. С этой целью все результаты располагают в порядке возрастания их значений: х1, х2,, …., хn-1, хn, т.е. представляют в виде упорядоченной выборки. Так как грубо ошибочными могут являться либо наименьшее значение х1, либо наибольшее хn, либо х1 и хn одновременно, то для первой и последней вариант выборки необходимо рассчитать значения Q-критерия:
10, как правило, используют так называемый Q–тест. С этой целью все результаты располагают в порядке возрастания их значений: х1, х2,, …., хn-1, хn, т.е. представляют в виде упорядоченной выборки. Так как грубо ошибочными могут являться либо наименьшее значение х1, либо наибольшее хn, либо х1 и хn одновременно, то для первой и последней вариант выборки необходимо рассчитать значения Q-критерия:

 ,
,
где xn–x1 – размах варьирования.
Полученные значения Q сравнивают с табличным значением для данного объема выборки при доверительной вероятности 90% (табл.2).
Таблица 2
Численные значения Q-критерия при доверительной вероятности Р и объеме выборки n
| Р | n | |||||||
| 90% | 0, 94 | 0, 76 | 0, 64 | 0, 56 | 0, 51 | 0, 47 | 0, 44 | 0, 41 |
| 95% | 0, 98 | 0, 85 | 0, 73 | 0, 64 | 0, 59 | 0, 54 | 0, 51 | 0, 48 |
| 99% | 0, 99 | 0, 93 | 0, 82 | 0, 74 | 0, 68 | 0, 63 | 0, 60 | 0, 57 |
Если Q1 или Qn окажется больше соответствующего табличного значения при данном n, то соответственно х1 или хn исключается из выборки как грубо ошибочный результат. Для оставшихся n-1 значений повторяют Q-тест. В том случае, когда и Q1, и Qn окажутся больше табличного значения, то промахами являются одновременно х1 и хn. После исключения их из выборки повторяют Q-тест до тех пор, пока не будут отброшены все результаты, полученные с недопустимо большими погрешностями.
После исключения промахов
а) рассчитывают среднее арифметическое значение ( ), отклонение каждой величины от среднего значения
), отклонение каждой величины от среднего значения  , квадраты отклонений
, квадраты отклонений  и представляют результаты в виде таблицы
и представляют результаты в виде таблицы
| № | Определяемая величина

| Отклонение от среднего

| Квадрат отклонения

|
| n |

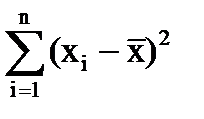
б) находят стандартное отклонение выборки S;
в) рассчитывают стандартное отклонение среднего  ;
;
г) находят полуширину доверительного интервала для среднего

при доверительной вероятности Р = 95% и числе степеней свободы 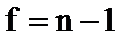 .
.
Окончательный результат анализа представляется в виде доверительного интервала:  .
.
Воспроизводимость определения характеризуется величиной доверительного интервала и относительным стандартным отклонением  Чем меньше доверительный интервал и относительное стандартное отклонение, тем лучше воспроизводимость данного определения.
Чем меньше доверительный интервал и относительное стандартное отклонение, тем лучше воспроизводимость данного определения.
При условии отсутствия систематических погрешностей относительная (процентная) погрешность определения вычисляется по формуле:
 .
.
Анализ выполнен правильно, если действительное значение определяемой величины " Т" не выходит за пределы доверительного интервала, найденного для среднего результата анализа при доверительной вероятности Р = 95%, а относительное стандартное отклонение Sr меньше или равно 0, 5%.
Если же действительное значение " Т" выходит за пределы доверительного интервала, то имеет место систематическая погрешность. Относительная (процентная) систематическая погрешность вычисляется по формуле:
 .
.