
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод минимальных путей и сечений
|
|
Вряде случаев для анализа надежности сложной системы бывает достаточным определить граничные оценки надежности сверху и снизу.
При оценке вероятности безотказной работы сверху определяют минимальные наборы работоспособных элементов (путей), обеспечивающих работоспособное состояние системы. При формировании пути, считая, что все элементы находятся в неработоспособном состоянии, последовательным переводом элементов вработоспособное состояние производят подбор вариантов соединений элементов, обеспечивающих наличие цепи.
Набор элементов образует минимальный путь, если исключение любого элемента из набора приводит к отказу пути. Из этого вытекает, что в пределах одного пути элементы находятся в основном соединении, а сами пути включаются параллельно.

Рис. 3.1. Мостиковая схема соединения элементов
Так, для рассмотренной мостиковой схемы (см. рис. 3.1) набор минимальных путей представлен на рис. 3.2. Поскольку один и тот же элемент включается в два параллельных пути, то в результате расчета получается оценка безотказности сверху:
 .
.
При определении минимальных сечений осуществляется подбор минимального числа элементов, перевод которых из работоспособного состояния в неработоспособное вызывает отказ системы. При правильном подборе элементов сечения возвращение любого из элементов в работоспособное состояние восстанавливает работоспособное состояние системы. Поскольку отказ каждого из сечений вызывает отказ системы, то первые соединяются последовательно. В пределах каждого сечения элементы соединяются параллельно, так как для работы системы достаточно наличия работоспособного состояния любого из элементов сечения.
Схема минимальных сечений для мостиковой схемы приведена на рис. 3.3. Поскольку один и тот же элемент включается в два сечения, то полученная оценка является оценкой снизу:
 .
.

Рис. 3.2. Набор минимальных путей

Рис. 3.3. Набор минимальных сечений
В рассматриваемом примере оценка безотказности снизу совпадает с фактической безотказностью, рассчитанной по первым двум методам.
Таким образом, при составлении минимальных путей и сечений любая система преобразуется в структуру с параллельно-последовательным или последовательно-параллельным соединением элементов.
5.Расчеты надежности сложных систем (преобразование треугольник-звезда)
Сущность этого приема поясняется с помощью рис.3.6. Исходя из основного критерия эквивалентного преобразования равенства ПН цепей «треугольника» и «звезды» между одинаковыми точками и учитывая правила перехода от ФАЛ к ВФ (3.4) - (3.6), можно для структуры, показанной на рис.3.6, составить систему уравнений:
 (3.7)
(3.7)

Рис.3.6
В результате решения системы уравнений (3.7) определяются значения ПН элементов эквивалентной «звезды»  . В частном случае, когда все элементы равнонадежны:
. В частном случае, когда все элементы равнонадежны:
 .
.
Если в исходной НФС может быть выделено несколько звеньев типа «треугольник», преобразование делают одновременно для всех звеньев, как это показано на рис.3.6.
Для упрощения расчетов значений  и
и  без существенной потери точности рекомендуется следующий прием. В системе уравнений (3.7) ПН р записываются через вероятности отказов
без существенной потери точности рекомендуется следующий прием. В системе уравнений (3.7) ПН р записываются через вероятности отказов  . Если в полученной новой системе уравнений пренебречь произведениями вида
. Если в полученной новой системе уравнений пренебречь произведениями вида  ,
,  ,
,  и
и  , то получим соотношения:
, то получим соотношения:
 ;
;  ;
;  (3.8)
(3.8)
Еще раз обратившись к рис.3.6, определим простое правило составления уравнений (3.8): выражение записывается обязательно для вероятностей отказа, причем этот показатель для элемента «звезды», присоединяемого к какой-либо вершине «треугольника», равен произведению показателей элементов «треугольника», прилегающих к этой же вершине. Для дальнейших расчетов делается обратный перевод показателей  в показатели
в показатели  , например,
, например,
 .
.
6.Расчеты надежности сложных систем (метод ключевого элемента).
Этот метод основан на использовании формулы полной вероятности. В сложной системе выделяется особый элемент, все возможные состояния Hi которого образуют полную группу,  . Если анализируемое состояние системы А, то его вероятность
. Если анализируемое состояние системы А, то его вероятность
 , (3.1)
, (3.1)
Второй сомножитель в (3.1) определяет вероятность состояния ^ А при условии, что особый элемент находится в состоянии Hi. Рассмотрение Hi -го состояния особого элемента как безусловного позволяет упростить структурную схему надежности и свести ее к последовательно-параллельному соединению элементов.
Так, в рассматриваемой мостиковой схеме (рис. 3.1) выделение элемента 5 в качестве особого с двумя возможными состояниями (1 — наличие и 2 —отсутствие цепи) Р{Н1}=р5; Р{Н2}=q5 позволяет от структурной схемы, представленной на рис. 3.1, перейти при безусловно исправном состоянии элемента 5 к схеме, представленной на рис. 3.4, а, При отказе элемента 5 структурная схема имеет вид, представленный на рис. 3.4, б. Если состояние А — наличие цепи между а и b, имеем:

 ;
;
 .
.

Рис. 3.4. Структурные схемы мостикового соединения элементов, соответствующих наличию (а) цепи в элементе 5 и ее отсутствию (б)
Сопоставление обоих методов расчета надежности показывает, что выделение особого элемента с последующим анализом упрощенных структурных схем существенно сокращает выкладки.
7.Расчеты надежности сложных систем (типовые случаи расчета надежности: последовательное, параллельное и смешанное соединение элементов)
8.Расчет надежности с использованием марковских случайных процессов
Пусть имеется некоторая система s. Говорят, что вsпроисходит случайный процесс, если он к стечением времени под влиянием случайных факторов (например, отказов и восстановлений отдельных компонентов) переходит из одного состояния в другое.
Такая система называется с дискретным состоянием, если она имеет конечное количество возможных состояний и переход из одного состояния в другое осуществляется скачком. Для описания случайного процесса, проистекающего в системе пользователя вероятностями состояний Р0(t), P1(t) …Pk(t) гдеPi(t) (i=0, …k) – вероятность того, что система в моментtнаходится в состоянииsi. 
Случайный процесс, протекающий в sназывается процессом в дискретном времени, если переходы из одного состояния возможны в определенные периоды времени. Если переходы возможны в любой момент времени, то процесс называется непрерывным.
Случайный процесс называется Марковским (если процесс без последствия) если все Р. процесса в будущем зависят от того, в котором состоянии находится процесс настоящем, и не зависят от того, каким образом этот процесс протекал в прошлом.
Марковский процесс представляет собой Марковскую цепь с k– различным состоянием и может быть предоставлен матрицей значений переходных вероятностей.

Марковская цепь в состоянии iна очередном шаге перейдет в состояниеj. Переход вероятности не зависит от номера шага, т.е. процесс перехода стационарен во времени то есть Марковская цепь является дискретным случайным процессом с дискретным временем из которого переход осуществляется через некоторый интервал времениDtиз одного состояния в другое счетное число состояний. Длительность пребывания в состоянииsiявляется случайной величиной для которогоFk(t) состояний. Все распределенияFk(t) подчинены экспоненциальному закону.
Марковский процесс обладает характерными свойствами, определенными в первую очередь экспоненциальными распределениями времени пребывания в каждом состоянии.
- Марковский процесс обладает свойством стационарного перехода в другую вероятность и длительность пребывания в том или ином состоянии не зависит от того в какой момент времени рассматривается этот процесс.
- Свойство оригинальности - за бесконечный промежуток времени не может произойти более одного перехода из одноного состояния в другое.
- Обладает свойством последствия.
Марковский процесс удобно описывать ориентировочно графом переходов вершины которого, представляют собой состояние, а) веса ребер соответствующих интенсивности перехода из одного состояния в другое. Зная переходную вероятность Pijи параметрliраспределение времени пребывания процесса вiсостоянии можно легко найти веса по формуле: lij=Pij·li.
Если при описании процесса перехода система из одного состояния в состояние сохраняет Марковское свойство, то пребывание Fk(t) подчиняется произвольному, не экспоненциальному закону, то такой процесс называется полумарковским или неоднородным Марковским процессом.
На основании графических переходов можно составить дифференциальные уравнения для нахождения вероятности пребывания Марковского процесса в состоянии Pi.
- Производная по tот пребывания системы в моментtв состоянииPiравна сумме произведений интенсивности переходов на составляющую вероятность. При этом слагаемым которые, соответствуют выходящим из одного состояния стрелки в другое приписывается знак “–”, а остальные состояния “+”. Общее число слагаемых равно числу входящих и выходящих.
Система дифференциальных уравнений содержит k– уравнений, но они зависимы, поэтому нужно дополнить их уравнением нормировки, которое показывает, что сумма событий полную группу равна 1.
Различают два типа случайных процессов:
а) при первом попадании в нерабочее состояние процесс прекращается (процесс с поглощающим экраном).
в) система находится в стационарном режиме отказов (с отражающим экраном).
Первый случай для не восстановимого изделия, а второй для изделия которое можно восстановить.
P1(t) – состояние работоспособности изделия.
Р2(t) – состояние отказов
l и mинтенсивность отказа и его восстановление.

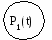
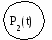


l
 m
m
;
Пусть Р1(0) = 1 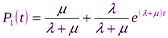
В стационарном режиме при t®¥ значение производной = 0. В результате получаем систему линейных алгоритмических уравнений. Это справедливо только для системы с отражающим экраном.
З
m
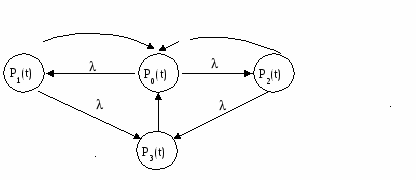 адана система дублирования с восстановлением:
адана система дублирования с восстановлением:
m


Pi= lim Pi(t) t®¥
i = 0, 1, 2, 3.
Р0+Р1+Р2+Р3 = 1
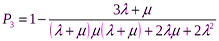 . k=P0 +P1+P2.
. k=P0 +P1+P2.
Для системы с поглощающим экраном стационарный режим не существует и с ростом времени вероятность для такой системы попасть в поглощающее состояние ®1.

 ;
;  ;
; 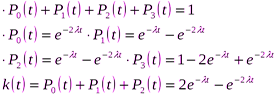
P0= 1
P1= 0
P2= 0
P3= 0
9.Резервирование. Классификация
| Признак классификации | Вид резервирования и резерва |
| Способ включения резерва | Постоянное резервирование. Резервирование замещением |
| Кратность резервирования | Однократное резервирование Многократное резервирование |
| Схема включения резерва | Общее резервирование Раздельное резервирование |
| Состояние резерва | Ненагруженный резерв Облегченный резерв Нагруженный резерв |
| Характеристика резерва | Восстанавливаемый резерв Невосстанавливаемый резерв |
| Фиксация резерва | Фиксированное резервирование. Скользящее резервирование |
| Однородность резервирования | Однородное резервирование. Смешанное резервирование |
Функциональное резервирование — метод повышения надежности объекта, предусматривающий использование способности элементов выполнять дополнительные функции.
Нагрузочное резервирование — метод повышения надежности объекта, предусматривающий использование избыточности по его способности к восприятию нагрузок.
Основной элемент —элемент структуры объекта, минимально необходимой для обеспечения его работоспособности.
Резервный элемент — элемент, предназначенный для обеспечения работоспособности объекта в случае отказа основного элемента.
Общее резервирование — резервирование, при котором резерв предусматривается на случай отказа объекта в целом.
Раздельное резервир ование — резервирование, при котором резерв предусматривается на случай отказов отдельных элементов объекта или их групп.
Смешанное резервирование — резервирование, при котором имеет место совмещение различных видов резервирования в одном объекте.
Однородное резервирование — резервирование, при котором в одном объекте используется лишь один вид резервирования.
Постоянное резервирование — резервирование, при котором резервные элементы участвуют в функционировании объекта наравне с основными.
Резервирование замещением — резервирование, при котором функции основного элемента передаются резерву только после отказа основного элемента.
Скользящее резервирование — резервирование замещением, при котором группа основных элементов объекта резервируется одним или несколькими резервными элементами, каждый из которых может заменить любой отказавший основной элемент в данной группе.
Фиксированное резервирование — резервирование, при котором место подключения каждого резервного элемента строго определено заранее.
Нагруженный резерв — резервный элемент, находящийся в том же рабочем режиме, что и основной элемент.
Облегченный резерв — резервный элемент, находящийся в менее нагруженном рабочем режиме, чем основной.
Ненагруженный резерв — резервный элемент, практически не несущий нагрузок.
Восстанавливаемый резерв — резервный элемент, работоспособность которого в случае отказа подлежит восстановлению.
Невосстанавливаемый ре зерв — резервный элемент, работоспособность которого в случае отказа не подлежит восстановлению.
Кратность резервирования — отношение числа резервных элементов к числу резервируемых элементов объекта.
Однократное резервирование (дублирование) —резервирование, кратность которого равна единице.
Многократное резервирование — резервирование, кратность которого выражается числом, большим единицы.
Резервирование с восстановлением — резервирование, при котором работоспособность любого основного и резервного элементов объекта в случаях возникновения их отказов подлежит восстановлению.
Резервирование без восстановления — резервирование, при котором работоспособность любого основного и резервного элементов объекта в случаях возникновения их отказов восстановлению не подлежит.
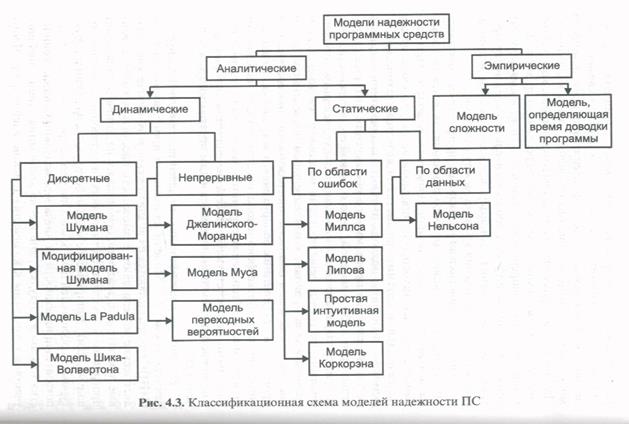
10.Надежность ПО. Модели. Классификация
Основным средством определения количественных показателей надежности являются модели надежности, под которыми понимают математические модели, построенные для оценки зависимости надежности от заранее известных или оцененных в ходе создания программного средства параметров. В связи с этим определение надежности показателей принято рассматривать в единстве трех процессов — предсказание, измерение, оценивание.
Предсказание — определение количественных показателей надежности исходя из характеристик будущего программно-информационного продукта.
Измерение— определение количественных показателей надежности, основанное на анализе данных об интервалах между отказами, полученных при выполнении программных заданий в условиях тестовых испытаний.
Оценивание— определение количественных показателей надежности, основанное на данных об интервалах между отказами, полученных в процессе испытания ПО и ИО АСОИУ в реальных условиях функционирования.
11.Надежность проекта
тетрадь
12.Факторы, влияющие на надежность
тетрадь
13.Техническое обслуживание и ремонт
тетрадь
14.Методы повышения надежности
Все методы повышения надежности технических средств систем могут быть сведены к следующим:
- резервирование;
- уменьшение интенсивности отказов технических средств;
- сокращение времени непрерывной работы;
- уменьшение среднего времени восстановления.
Реализация указанных методов может осуществляться либо при проектировании, либо при изготовлении, либо в процессе эксплуатации технических средств.
Уменьшить среднее время восстановления можно, повышая надежность технических средств и тем самым, уменьшая число отказов, или сокращая время, необходимое для отыскания и устранения отказов. Сократить время, необходимое для отыскания и устранения неисправностей, можно, применяя встроенный контроль, автоматизацию проверок, повышение квалификации обслуживающего персонала, сбор и обобщение опыта эксплуатации.
Уменьшить время непрерывной работы объектов можно в том случае, если имеется возможность выключать объекты на определенные промежутки времени.
Наиболее эффективными и многочисленными методами повышения надежности, являются методы, которые применяются при проектировании технических средств. К таким методам относятся:
- резервирование;
- выбор наиболее надежных элементов;
- создание схем с ограниченными последствиями отказов элементов;
- облегчение электрических, механических, тепловых и других режимов работы элементов;
- стандартизация и унификация элементов и узлов;
- встроенный контроль;
- автоматизация проверок.
Эффективность этих методов состоит в том, что они принципиально позволяют из малонадежных элементов строить надежные объекты и системы. Эти методы позволяют уменьшить интенсивность отказов объектов и систем, уменьшить среднее время их восстановления и время непрерывной работы.
Повысить надежность системы в процессе ее эксплуатации чрезвычайно трудно. Это объясняется тем, что надежность системы в основном закладывается в процессе ее проектирования и изготовления. При эксплуатации системы ее надежность уменьшается, причем скорость ее снижения зависит от методов эксплуатации, квалификации обслуживающего персонала и условий эксплуатации.
15.Испытания на надежность
Испытания на надежность – обязательный вид испытаний. Общая их цель – установить, какой надежностью обладают изделия в условиях, предписываемых методикой испытаний.
Испытания на надежность проводятся как комплекс мероприятий по определению показателей надежности на этапах производства и проектирования, а также с целью контроля надежности разрабатываемых и выпускаемых РЭС (ЭВС).
Объектом испытаний является партия изделий, из которой берется выборка (sample).
С испытаниями на надежность связаны некоторые проблемы.
Во первых, эти испытания требуют больших затрат времени и средств; во-вторых, в процессе их проведения расходуется часть ресурса изделий; в третьих, есть проблема доверия результатам испытаний.
Испытания (И) на надежность, в зависимости от цели проведения, подразделяют на определительные и контрольные.
Определительные И на надежность проводятся для установления показателей надежности изделий. Эти показатели (прежде всего, среднее время наработки до отказа, вероятность безотказной работы за назначенное время, интенсивность отказов, средняя наработка на отказ) включают затем в нормативно-техническую документацию на изделие.
Большое значение при проведении определительных И имеет верный выбор параметров, информирующих о состоянии изделия (работает или отказывает).
Контрольные И на надежность проводятся для контроля соответствия или несоответствия партии изделий заданному уровню надежности. По результатам этих И объект испытаний (партию изделий) относят – с заданным риском - либо к категории годных либо негодных по уровню их надежности.
Используют и специальные виды испытаний на надежность, такие как:
- испытания на срок службы;
- ускоренные испытания на срок службы;
- испытания на (не)разрушающие под влиянием определенных факторов.
При ускоренных испытаниях все в принципе делается как и при неускоренных испытаниях, но при повышенных нагрузках (электрических, тепловых и др.)
При испытаниях на разрушение нагрузку увеличивают до тех пор, пока это не вызовет отказ изделия.
Испытания классифицируют и еще по ряду признаков:
- стадии создания или эксплуатации объектов;
- месту и условиям проведения (лабораторные, испытания в условиях эксплуатации…);
- по используемым методам и аппаратуре (моделирование, натурный эксперимент);
- по уровню объектов (комплектующих элементов, отдельных устройств, систем).
Результаты определительных И представляются в виде:
- статистики отказов ипытываемых объектов;
- множества значений выходных параметров объектов;
- характеристик наблюдаемых изменений физико-химических процессов в материалах объектов.