Метод средних величин, виды и формы средних величин, методы их расчета

Средняя величина – это обобщающий показатель, характеризующий однотипные общественные явления по одному количественному признаку в конкретных условиях места и времени. Например, ср/месяч. з/п, средняя продолжительность жизни, средняя урожайность. Средняя показывает уровень признака отнесенный к единице совокупности. Например, средняя урожайность, средняя заработная плата, среднее количество выпавших осадков, средняя продолжительность жизни и т.д. Сравнивая во времени изменение средних уровней в одних и тех же совокупностях, ст. тем самым определяет закономерности развития социально-экономических явлений, т.е. в этих изменениях проявляется общая тенденция (типичность) развития явления. Первым условием применения средних величин является: все средние должны опираться на массовые общественные явления. Вторым условием - групповые средние должны дополняться общими средними.Третьим - все показатели средних должны определяться по однородной совокупности.

Обычно средние показатели ст. определялись как среднее арифметическое в том случае, когда были указаны индивидуальные значения признака. Если в совокупности признаки имеют частоту повторения (вес), то в этом случае среднее арифметическое принимало форму взвешенной, т.о. среднее рассчитывается в виде арифметической, но в форме простой и взвешенной. Например, з/п 5 рабочих составляет 400, 420, 480, 510, 550. Чтоб определить среднюю з/п 1 рабочего, нужно сложить все показатели и разделить на 5. Показателем з/п будет являться x1, x2, …, x5. Отсюда формула:

Средняя арифметическая простая равна сумме показателей (уровней), деленной на число показателей (уровней).

Средняя арифметическая взвешенная принимается в тех случаях, когда известны отдельные значения признака и их веса (fi), т.е. частота повторения признака.

Средняя арифметическая взвешенная равна сумме произведений признака на вес, деленной на сумму веса.

В этой формуле числитель дроби выражает прямую зависимость в результате чего, получается реальный экономический смысл.

В расчетах средней арифметической взвешенной применяются следующие методы (приемы):

Если значение X уменьшить в одно и то же число раз, то занчение средней увеличится в это же число раз.

Если значение X увеличить в одно и то же количество раз, то значение средней уменьшится это же количество раз;

Если все значения веса f изменить в несколько раз, то значение средней не изменится.

Если для решения задачи используется 3 метода (приема), то эта задача решена способом моментов.

Вторым видом средних величин является средняя гармоническая, которая применяется в двух формах: простой и взвешенной.

Средняя гармоническая применяется в тех случаях, когда известно отдельные значения признака X и объемы признаков.

Объемом может быть: фонд з/п, валовой сбор, сумма товарооборота, стипендиальный фонд, фактический выпуск продукции. В этой формуле наблюдается обратная связь, т.е. при делении 2-ух показателей получается 3 имеющий экономический смысл. Например, при делении фактического товарооборота на количество проданных товаров мы получим цену товара.

Формула средней гармонической простой:

Эта формула обратная средней арифметической простой и предполагается, что сумма объемов в данном случае равна единице.

Средняя гармоническая взвешенная:

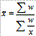
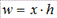
Средняя гармоническая взвешенная равна сумме объемов признаков деленная на сумму отношения объема к признаку.

Средняя квадратическая:

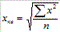
Средняя кубическая: