Показатели вариации и их значение, методика их расчета.

В практическом анализе оценка рассеяния значений признака может оказаться не менее важной, чем определение средней.

Самая грубая оценка рассеяния, легко определяемая по данным вариационного ряда, может быть дана с помощью размаха вариации –характеризует границы вариации изучаемого признака.

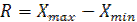
где xmax и xmin - наибольшее и наименьшее значения варьиру­ющего признака.

Показывает, на сколько велико различие между единицами совокупности, имеющими самое маленькое и самое большое значение признака. Показатель основан на крайних значениях варьирующего признака и не отражает отклонений всех вариант в ряду.

Однако этот показатель не дает представления о характере вариационного ряда, расположении вариантов вокруг средней и может сильно меняться, если добавить или исключить крайние варианты (когда эти значения аномальны для данной совокуп­ности). В этих случаях размах вариации дает искаженную амплиту­ду колебания против нормальных ее размеров. Поэтому следует очистить совокупность от аномальных наблюдений, прежде чем определять размах вариации.

Для оценки колеблемости значений признака относительно средней используются характеристики рассеяния. Они различают­ся выбранной формой средней и способами оценки отклонений от нее отдельных вариантов. К таким показателям относятся:

- среднее линейное отклонение;

- дисперсия;

- среднее квадратическое отклонение;

- коэффициент вариации.

Среднее линейное отклонение есть средняя арифметическая из абсолютных значений отклонений отдельных вариантов от их средней величины:

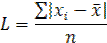для не сгруппированных данных

для сгруппированных данных

где xi - значение признака в дискретном ряду или середина ин­тервала в интервальном распределении;

fi - частота признака.

Среднее линейное отклонение выражено в тех же единицах из­мерения, что и варианты или их средняя. Оно дает абсолютную меру вариации. Показывает, на какую величину отклоняется признак в изучаемой совокупности от средней величины признака.

Чтобы избежать равенства нулю суммы отклонений от сред­ней, используют либо абсолютные значения отклонений, либо их четные степени, например квадраты. В последнем случае мера ва­риации называется дисперсией и обозначается D или s2:

Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средних величин. В зависимости от исходных данных вычисляется по формулам:

для несгруппированных данных

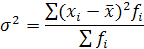для сгруппированных данных

Расчет дисперсии может быть упрощен.

или

Вследствие суммирования квадратов отклонений дис­персия дает искаженное представление об отклонениях, измеряя их в квадратных единицах. Поэтому на основе дисперсии вводят­ся еще две характеристики: среднее квадратическое отклонение и коэффициент вариации.

Среднее квадратическое отклонение измеряется в тех же едини­цах, что и варьирующий признак, и исчисляется путем извлече­ния квадратного корня из дисперсии:

для несгруппированных данных

для сгруппированных данных

Среднее квадратическое отклонение, как и среднее линейное отклонение, показывает, на сколько в среднем отклоняются кон­кретные варианты признака от его среднего значения. Величина о часто используется в качестве единицы измерения отклонений от средней арифметической. Отклонение, выраженное в s, называ­ется нормированным или стандартизированным.

Коэффициент вариации – характеризует меру вариации значений признака вокруг средней величины. Дает относительную оценку вариации и получается путем сопоставления среднего линейного или среднего квадратического отклонения со средним уровнем явления, а результат выражается в процентах:

Чем коэффициент меньше, тем однороднее совокупность и наоборот, чем больше тем неоднороднее.

Так как коэффициенты вариации дают относительную харак­теристику однородности явлений и процессов, они позволяют сравнивать степень вариации разных признаков.

или Линейный коэффициент вариации

Коэффициент осциляции