
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Стадии и этапы создания АС 6 страница
|
|
Мы видим, что спектр является комплексной функцией. Первая точка спектра  является суммой отсчетов входного сигнала, деленной на
является суммой отсчетов входного сигнала, деленной на  , т.е средним значением всех отсчетов, поскольку
, т.е средним значением всех отсчетов, поскольку  ,
,  . Дальнейшие значения спектра содержат как действительную, так и мнимую части, они получаются умножением значений сигнала на соответствующие значения синуса и косинуса. Часто при вычислении спектра ограничиваются только действительной составляющей.
. Дальнейшие значения спектра содержат как действительную, так и мнимую части, они получаются умножением значений сигнала на соответствующие значения синуса и косинуса. Часто при вычислении спектра ограничиваются только действительной составляющей.
Для восстановления сигнала по заданной спектральной функции применяется обратное дискретное преобразование Фурье:
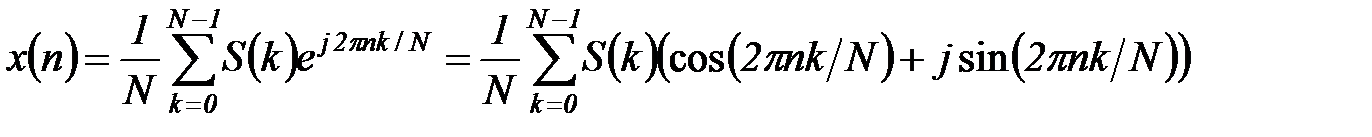 . (5.53)
. (5.53)
Для упрощения записи формул (4.52) и (4.53) введем следующее обозначение:
 .
.
Тогда коэффициенты в (4.52) примут вид 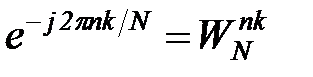 ,
,
а само дискретное преобразование Фурье (4.52) запишется в виде суммы:
 ,
, 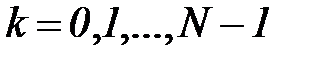 . (5.54)
. (5.54)
Обратим внимание на периодический характер коэффициентов  :
:
 ;
;  в силу того, что
в силу того, что  ,
,  . (4.55)
. (4.55)
Для вычисления всего спектра дискретного сигнала в соответствии с формулой (5.52) требуется  операций умножения и
операций умножения и  операций сложения комплексных чисел, что при больших размерах сигналов составляет проблемы даже для современных компьютеров. Для снижения трудоемкости вычислений широко используется алгоритм так называемого быстрого преобразования Фурье (БПФ) [11]. Рассмотрим идею этого алгоритма на примере обработки дискретной выборки из восьми отсчетов (
операций сложения комплексных чисел, что при больших размерах сигналов составляет проблемы даже для современных компьютеров. Для снижения трудоемкости вычислений широко используется алгоритм так называемого быстрого преобразования Фурье (БПФ) [11]. Рассмотрим идею этого алгоритма на примере обработки дискретной выборки из восьми отсчетов ( ).
).
Выпишем выражения для всех значений спектра в соответствии с (5.52):
 (5.56)
(5.56)
В этих выражениях для простоты опущен масштабный множитель 1/8.
В соответствии с законом периодичности (5.55) между коэффициентами  имеют место следующие равенства:
имеют место следующие равенства:
 (5.57)
(5.57)
Таким образом, все множители в спектральном разложении могут быть выражены всего через четыре коэффициента:  .
.
Подставив в выражения для значений спектра (5.56) соотношения (5.57) и приведя подобные члены, получим
 (5.58)
(5.58)
Сравнивая выражения (5.56) и (5.58), мы можем оценить выигрыш в количестве операций. Если в первом случае требовалось 64 операции умножения и 64 операции сложения, то во втором число операций соответственно составляет 22 операции умножения и 48 операций сложения/вычитания, причем это число можно еще уменьшить при дальнейшем совершенствовании алгоритма. В частности, можно заметить, что переменные группируются – сначала по 2:  , затем по 4 – на четные и нечетные и, наконец, по 8. Учитывая эту закономерность, можно уменьшить число сложений/вычитаний.
, затем по 4 – на четные и нечетные и, наконец, по 8. Учитывая эту закономерность, можно уменьшить число сложений/вычитаний.
Полученным выигрышем и определяется название алгоритма.
Наиболее эффективно алгоритм БПФ работает, когда число элементов дискретного сигнала представляет собой целую степень числа 2, т.е.  , где
, где 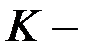 целое число.
целое число.
При увеличении размера массива исходных данных эффективность алгоритма быстрого преобразования Фурье резко возрастает. Так, при  эффективность этого алгоритма составляет приблизительно 1: 200 по сравнению со схемой (5.56). Алгоритм быстрого преобразования Фурье реализован во многих математических и статистических пакетах программ. Кроме того, в Интернете можно найти программы БПФ на основных языках программирования.
эффективность этого алгоритма составляет приблизительно 1: 200 по сравнению со схемой (5.56). Алгоритм быстрого преобразования Фурье реализован во многих математических и статистических пакетах программ. Кроме того, в Интернете можно найти программы БПФ на основных языках программирования.
При практическом использовании алгоритма БПФ нужно помнить, что он вычисляет все  компонентов спектра
компонентов спектра  ,
,  . Если требуемое количество компонентов спектра невелико, то может оказаться более удобным исходный алгоритм (5.52).
. Если требуемое количество компонентов спектра невелико, то может оказаться более удобным исходный алгоритм (5.52).
5.4.2 Вейвлет - преобразования сигналов
Принцип вейвлет-преобразования. Гармонические базисные функции преобразования Фурье предельно локализованы в частотной области и не локализованы во временной (они определены во всем временном интервале от -¥ до +¥). Их противоположностью являются импульсные базисные дельта-функции типа импульсов Кронекера, которые предельно локализованы во временной области и «размыты» по всему частотному диапазону. Вейвлеты (wavelet – короткая волна) по локализации в этих двух представлениях можно рассматривать как функции, занимающие промежуточное положение между гармоническими и импульсными функциями. Они должны быть локализованными как во временной, так и в частотной области представления. Однако при проектировании таких функций мы неминуемо столкнемся с известным принципом неопределенности, связывающим эффективные значения длительности функций и ширины их спектра. Чем точнее мы будем осуществлять локализацию временного положения функции, тем шире будет становиться ее спектр, и наоборот. Отличительной особенностью вейвлет-анализа является то, что в нем можно использовать семейства функций, реализующих различные варианты соотношения неопределенности. Соответственно, исследователь имеет возможность гибкого выбора между ними и применения тех вейвлетных функций, которые наиболее эффективно решают поставленные задачи [11].
Вейвлетный базис пространства L2(R), R (-¥, +¥), целесообразно конструировать из финитных функций, принадлежащих этому же пространству, которые должны стремиться к нулю на бесконечности. Чем быстрее эти функции стремятся к нулю, тем удобнее использовать их в качестве базиса преобразования при анализе реальных сигналов. Допустим, что такой функцией является psi - функция  , равная нулю за пределами некоторого конечного интервала и нулевое среднее значение по интервалу задания. Последнее необходимо для задания определенной локализации спектра вейвлета в частотной области. На основе этой функции сконструируем базис в пространстве L2(R) с помощью масштабных преобразований независимой переменной. Простейшим примером такого базиса могут служить функции Хаара
, равная нулю за пределами некоторого конечного интервала и нулевое среднее значение по интервалу задания. Последнее необходимо для задания определенной локализации спектра вейвлета в частотной области. На основе этой функции сконструируем базис в пространстве L2(R) с помощью масштабных преобразований независимой переменной. Простейшим примером такого базиса могут служить функции Хаара  , рассмотренные в разделе 5.2.
, рассмотренные в разделе 5.2.
Функция изменения частотной независимой переменной в спектральном представлении сигналов отображается во временном представлении растяжением/сжатием сигнала. Для вейвлетного базиса это можно выполнить функцией типа  ,
,  ,
,  , т.е. путем линейной операции растяжения/сжатия, обеспечивающей самоподобие функции на разных масштабах представления. Однако конечность (локальность) функции
, т.е. путем линейной операции растяжения/сжатия, обеспечивающей самоподобие функции на разных масштабах представления. Однако конечность (локальность) функции  на временной оси требует дополнительной независимой переменной последовательных переносов (сдвигов) функции
на временной оси требует дополнительной независимой переменной последовательных переносов (сдвигов) функции  вдоль оси (параметра локализации), типа
вдоль оси (параметра локализации), типа  , для перекрытия всей числовой оси пространства R (-¥, +¥). C учетом обеих условий одновременно структура базисной функции может быть принята следующей:
, для перекрытия всей числовой оси пространства R (-¥, +¥). C учетом обеих условий одновременно структура базисной функции может быть принята следующей:
 . (5.59)
. (5.59)
Для упрощения дальнейших выкладок значения переменных m и k примем целочисленными. При приведении функции (4.59) к единичной норме, получаем:
 . (5.60)
. (5.60)
Если для семейства функций  выполняется условие ортогональности:
выполняется условие ортогональности:
 (5.61)
(5.61)
то семейство  может использоваться в качестве ортонормированного базиса пространства L2(R). Отсюда следует, что произвольная функция этого пространства может быть представлена в виде ряда (разложения по базису
может использоваться в качестве ортонормированного базиса пространства L2(R). Отсюда следует, что произвольная функция этого пространства может быть представлена в виде ряда (разложения по базису  ):
):
 , (5.62)
, (5.62)
где коэффициенты представления сигнала – проекции сигнала на новый ортогональный базис функций, как и в преобразовании Фурье, определяются скалярным произведением
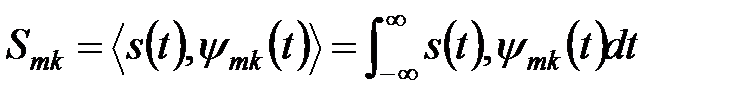 (5.63)
(5.63)
при этом ряд равномерно сходиться, то есть
 .
.
При выполнении этих условий базисная функция преобразования  называется ортогональным вейвлетом.
называется ортогональным вейвлетом.
В основе вейвлет-преобразований, в общем случае, лежит использование двух непрерывных, взаимозависимых и интегрируемых по независимой переменной функций:
Вейвлет-функции  , как psi- функции времени с нулевым значением интеграла и частотным фурье-образом
, как psi- функции времени с нулевым значением интеграла и частотным фурье-образом  . Этой функцией, которую обычно и называют вейвлетом, выделяются детали сигнала и его локальные особенности. Пример временного и частотного образа функции приведен на рисунке 5.10.
. Этой функцией, которую обычно и называют вейвлетом, выделяются детали сигнала и его локальные особенности. Пример временного и частотного образа функции приведен на рисунке 5.10.
Масштабирующей функции  , как временной скейлинг-функции phi с единичным значением интеграла, с помощью которой выполняется грубое приближение (аппроксимация) сигнала.
, как временной скейлинг-функции phi с единичным значением интеграла, с помощью которой выполняется грубое приближение (аппроксимация) сигнала.

Рисунок 5.10. Вейвлетные функции в двух масштабах.
Phi -функции присущи не всем, а, как правило, только ортогональным вейвлетам. Они необходимы для преобразования не центрированных и достаточно протяженных сигналов при раздельном анализе низкочастотных и высокочастотных составляющих. Роль и использование phi-функции рассмотрим несколько позже.
Непрерывное вейвлет-преобразование. Допустим, что мы имеем функции  с конечной энергией (нормой) в пространстве
с конечной энергией (нормой) в пространстве  , определенные по всей действительной оси R (-¥, ¥). Для финитных сигналов с конечной энергией средние значения сигналов, как и любых других функций из пространства
, определенные по всей действительной оси R (-¥, ¥). Для финитных сигналов с конечной энергией средние значения сигналов, как и любых других функций из пространства  , должны стремиться к нулю на ±¥.
, должны стремиться к нулю на ±¥.
Непрерывным вейвлет-преобразованием (или вейвлетным образом) функции  называют функцию двух переменных:
называют функцию двух переменных:
 ,
,  ,
,  (5.64)
(5.64)
где вейвлеты  – масштабированные и сдвинутые копии порождающего вейвлета
– масштабированные и сдвинутые копии порождающего вейвлета 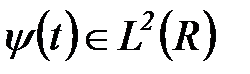 , совокупность которых создает новый базис пространства
, совокупность которых создает новый базис пространства  .
.
Порождающими функциями могут быть самые различные функции, ограниченные по времени и местоположению на временной оси, и имеющие спектральный образ, в определенной степени локализованный на частотной оси. Как и для рядов Фурье, базис пространства  целесообразно конструировать из одной порождающей функции, норма которой должна быть равна 1. Для перекрытия локальной функцией вейвлета всей временной оси пространства используется операция сдвига (смещения по временной оси):
целесообразно конструировать из одной порождающей функции, норма которой должна быть равна 1. Для перекрытия локальной функцией вейвлета всей временной оси пространства используется операция сдвига (смещения по временной оси):  , где значение b для непрерывного вейвлет-преобразования также является величиной непрерывной. Для перекрытия всего частотного диапазона пространства
, где значение b для непрерывного вейвлет-преобразования также является величиной непрерывной. Для перекрытия всего частотного диапазона пространства  используется операция временного масштабирования вейвлета с непрерывным изменением независимой переменной:
используется операция временного масштабирования вейвлета с непрерывным изменением независимой переменной:  . На рисунке 5.10 видно, что если временной образ вейвлета будет расширяться (изменением значения параметра a), то его «средняя частота» будет понижаться, а частотный образ (частотная локализация) перемещаться на более низкие частоты. Таким образом, путем сдвига по независимой переменной
. На рисунке 5.10 видно, что если временной образ вейвлета будет расширяться (изменением значения параметра a), то его «средняя частота» будет понижаться, а частотный образ (частотная локализация) перемещаться на более низкие частоты. Таким образом, путем сдвига по независимой переменной  вейвлет имеет возможность перемещаться по всей числовой оси произвольного сигнала, а путем изменения масштабной переменной a (в фиксированной точке
вейвлет имеет возможность перемещаться по всей числовой оси произвольного сигнала, а путем изменения масштабной переменной a (в фиксированной точке  временной оси) «просматривать» частотный спектр сигнала по определенному интервалу окрестностей этой точки.
временной оси) «просматривать» частотный спектр сигнала по определенному интервалу окрестностей этой точки.
С использованием этих операций вейвлетный базис функционального пространства образуется путем масштабных преобразований и сдвигов порождающего вейвлета  :
:
 ,
,  ,
,  ,
,  (5.65)
(5.65)
Нетрудно убедиться, что нормы вейвлетов  равны норме
равны норме  , что обеспечивает нормировочный множитель
, что обеспечивает нормировочный множитель  . При нормировке к 1 порождающего вейвлета
. При нормировке к 1 порождающего вейвлета  все семейство вейвлетов также будет нормированным. Если при этом выполняется требование ортогональности функций, то функции
все семейство вейвлетов также будет нормированным. Если при этом выполняется требование ортогональности функций, то функции  будут представлять собой ортонормированный базис пространства
будут представлять собой ортонормированный базис пространства  .
.
Так как форма базисных функций  зафиксирована, то вся информация о сигнале в (5.64) переносится на значения функции c(a, b). Точность обратного интегрального вейвлет-преобразования зависит от выбора базисного вейвлета и способа построения базиса, т.е. от значений базисных параметров a, b. Строго теоретически вейвлет может считаться базисной функцией
зафиксирована, то вся информация о сигнале в (5.64) переносится на значения функции c(a, b). Точность обратного интегрального вейвлет-преобразования зависит от выбора базисного вейвлета и способа построения базиса, т.е. от значений базисных параметров a, b. Строго теоретически вейвлет может считаться базисной функцией  только в случае его ортонормированности. Для практических целей непрерывного преобразования часто бывает вполне достаточна устойчивость и «приблизительность» ортогональности системы разложения функций. Под устойчивостью понимается достаточно точная реконструкция произвольных сигналов. Для ортонормированных вейвлетов обратное вейвлет-преобразование записывается с помощью того же базиса, что и прямое:
только в случае его ортонормированности. Для практических целей непрерывного преобразования часто бывает вполне достаточна устойчивость и «приблизительность» ортогональности системы разложения функций. Под устойчивостью понимается достаточно точная реконструкция произвольных сигналов. Для ортонормированных вейвлетов обратное вейвлет-преобразование записывается с помощью того же базиса, что и прямое:
 . (5.66)
. (5.66)
где  - норммрующий коэффициент:
- норммрующий коэффициент:
 . (5.67)
. (5.67)
Рассмотрим примеры вейвлет-преобразований. На рисунке 5.11 приведен пример разложения сигнала  вейвлетом Хаара с тремя последовательными по масштабу m вейвлетными функциями с параметром
вейвлетом Хаара с тремя последовательными по масштабу m вейвлетными функциями с параметром 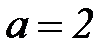 , при этом сам сигнал
, при этом сам сигнал  образован суммированием этих же вейвлетных функций с одинаковой амплитудой с разным сдвигом от нуля, как это показано на рисунке.
образован суммированием этих же вейвлетных функций с одинаковой амплитудой с разным сдвигом от нуля, как это показано на рисунке.

Рисунок 5.11. Скалярные произведения сигнала с вейвлетами Хаара.
На рисунке 5.12 приведен пример графического отображения вейвлетной поверхности реального физического процесса, полученного при использовании вейвлет-функций типа тех, что показаны на рисунке 5.10. При этом параметр a вейвлет-функции (отложен по вертикальной оси) изменяется непрерывно. Вид поверхности определяет изменения во времени спектральных компонент различного масштаба и называется частотно-временным спектром. Поверхность изображается на рисунках, как правило, в виде изолиний или условными цветами. Для расширения диапазона масштабов может применяться логарифмическая шкала.

Рисунок 5.12. Пример непрерывного вейвлет-преобразования сигнала
5.5 Анализ и прогнозирование временных рядов
В данном разделе мы коротко познакомимся с одним из важных информационных процессов – анализом и прогнозированием временных рядов
[24]. Временным рядом называется последовательность значений некоторой величины, измеренных в последовательные моменты времени. Временной ряд обычно рассматривают как случайную функцию дискретного времени, и для его анализа используют различные математические модели и методы, часть из которых рассмотрена выше.
Анализ временных рядов актуален во многих областях: в экономике, социологии, технике, в науке (экологии, астрономии и других).
Существуют две основные цели анализа временных рядов:
· определение природы ряда,
· прогнозирование (предсказание будущих значений временного ряда по настоящим и прошлым значениям).
Обе эти цели требуют, чтобы была создана формальная модель ряда. С ее помощью можно интерпретировать рассматриваемые данные (например, в задачах экономики выявлять сезонные изменения цен на товары, состояние финансовых рынков, прогнозировать цены на различные товары, курсы акций). Можно также экстраполировать ряд на основе имеющейся модели, т.е. предсказывать его будущие значения природных явлений. Такие задачи важны, например, при предсказании землетрясений, массовых пожаров, размножения вредителей и других природных катастроф