Вычисление электростатического поля бесконечной равномерно заряженной плоскости через теорему О-Г.

Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле:

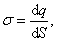
где d q – заряд, сосредоточенный на площади d S; d S – физически бесконечно малый участок поверхности.

Пусть σ во всех точках плоскости S одинакова. Заряд q – положительный. Напряженность во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).

Очевидно, что в симметричных, относительно плоскости точках, напряженность будет одинакова по величине и противоположна по направлению.

Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями Δ S, расположенными симметрично относительно плоскости (рис. 2.12).

Тогда

Применим теорему Остроградского-Гаусса. Поток Ф_Е через боковую часть поверхности цилиндра равен нулю, т.к. Для основания цилиндра

Суммарный поток через замкнутую поверхность (цилиндр) будет равен:

Внутри поверхности заключен заряд . Следовательно, из теоремы Остроградского–Гаусса получим:

;

откуда видно, что напряженность поля плоскости S равна:

(2.5.1)

Полученный результат не зависит от длины цилиндра. Это значит, что на любом расстоянии от плоскости

4) Вычисление электростатического поля бесконечно равномерно заряженного прямого кругового цилиндра (нити) с помощью теоремы О-Г.

Пусть поле создается бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной линейной плотностью , где d q – заряд, сосредоточенный на отрезке цилиндра (рис. 2.14).

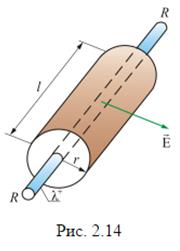
Из соображения симметрии следует, что Е в любой точке будет направлена вдоль радиуса, перпендикулярно оси цилиндра.

Представим вокруг цилиндра (нити) коаксиальную замкнутую поверхность (цилиндр в цилиндре) радиуса r и длиной l (основания цилиндров перпендикулярно оси). Для оснований цилиндров для боковой поверхности т.е. зависит от расстояния r.

Следовательно, поток вектора через рассматриваемую поверхность, равен

При на поверхности будет заряд 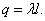По теореме Остроградского-Гаусса , отсюда

.

(2.5.6)

Если , т.к. внутри замкнутой поверхности зарядов нет (рис.2.15).

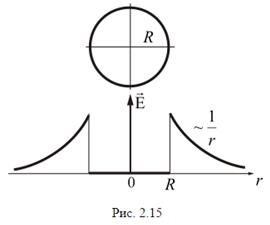
Если уменьшать радиус цилиндра R (при 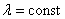), то можно вблизи поверхности получить поле с очень большой напряженностью и, при , получить нить.