
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Если магнитное поле создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником в отдельности.
|
|
Индукцию 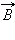 проводника с током можно представить как векторную сумму элементарных индукций
проводника с током можно представить как векторную сумму элементарных индукций  создаваемых отдельными участками проводника. На опыте невозможно выделить отдельный участок проводника с током, так как постоянные токи всегда замкнуты. Можно измерить только суммарную индукцию магнитного поля, создаваемого всеми элементами тока. Закон Био–Савара определяет вклад
создаваемых отдельными участками проводника. На опыте невозможно выделить отдельный участок проводника с током, так как постоянные токи всегда замкнуты. Можно измерить только суммарную индукцию магнитного поля, создаваемого всеми элементами тока. Закон Био–Савара определяет вклад  в магнитную индукцию
в магнитную индукцию 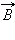 результирующего магнитного поля, создаваемый малым участком Δ l проводника с током I.
результирующего магнитного поля, создаваемый малым участком Δ l проводника с током I.
|
Здесь r – расстояние от данного участка Δ l до точки наблюдения, α – угол между направлением на точку наблюдения и направлением тока на данном участке, μ 0 – магнитная постоянная. Направление вектора  определяется правилом буравчика: оно совпадает с направлением вращения рукоятки буравчика при его поступательном перемещении вдоль тока. Рис. 1.17.1 иллюстрирует закон Био–Савара на примере магнитного поля прямолинейного проводника с током. Если просуммировать (проинтегрировать) вклады в магнитное поле всех отдельных участков прямолинейного проводника с током, то получится формула для магнитной индукции поля прямого тока:
определяется правилом буравчика: оно совпадает с направлением вращения рукоятки буравчика при его поступательном перемещении вдоль тока. Рис. 1.17.1 иллюстрирует закон Био–Савара на примере магнитного поля прямолинейного проводника с током. Если просуммировать (проинтегрировать) вклады в магнитное поле всех отдельных участков прямолинейного проводника с током, то получится формула для магнитной индукции поля прямого тока:
|

Итак, вокруг всякого движущегося заряда помимо электрического поля существует еще и магнитное. Магнитное поле – это поле движущихся зарядов. Известно, что оно обнаруживает себя по действию на магнитные стрелки или на проводники с токами, т.е. на движущиеся заряды. магнитное поле – это одна из форм проявления электромагнитного поля, особенностью которого является то, что это поле действует только на движущиеся частицы и тела, обладающие электрическим зарядом, а также на намагниченные тела. Магнитное поле создается проводниками с током, движущимися электрическими заряженными частицами и телами, а также переменными электрическими полями. Возьмем такой контур с током I и поместим его в магнитное поле. Основное свойство магнитного поля – способность действовать на движущиеся электрические заряды с определенной силой. В магнитном поле контур с током будет ориентироваться определенным образом. Ориентацию контура в пространстве будем характеризовать направлением нормали 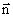 , связанной с движением тока правилом правого винта или «правилом буравчика» (рис. 1.2). Итак, на контур с током в магнитном поле действует вращающий момент. Контур ориентируется в данной точке поля только одним способом. Примем положительное направление нормали
, связанной с движением тока правилом правого винта или «правилом буравчика» (рис. 1.2). Итак, на контур с током в магнитном поле действует вращающий момент. Контур ориентируется в данной точке поля только одним способом. Примем положительное направление нормали 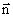 за направление магнитного поля
за направление магнитного поля 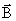 в данной точке. Вращающий момент прямо пропорционален величине тока I, площади контура S и синусу угла между направлением магнитного поля и нормали
в данной точке. Вращающий момент прямо пропорционален величине тока I, площади контура S и синусу угла между направлением магнитного поля и нормали 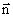 .
.

здесь М – вращающий момент, или момент силы,  – магнитный момент контура (аналогично
– магнитный момент контура (аналогично 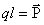 – электрический момент диполя).
– электрический момент диполя).

Направление вектора магнитного момента совпадает с положительным направлением нормали.
 (1.1.1)
(1.1.1)
Отношение момента силы к магнитному моменту  для данной точки магнитного поля будет одним и тем же и может служить характеристикой магнитного поля, названной магнитной индукцией:
для данной точки магнитного поля будет одним и тем же и может служить характеристикой магнитного поля, названной магнитной индукцией:
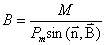 (1.1.2)
(1.1.2)
или 
где 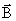 – вектор магнитной индукции, совпадающий с нормалью
– вектор магнитной индукции, совпадающий с нормалью 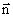 . По аналогии с электрическим полем
. По аналогии с электрическим полем  . Магнитная индукция
. Магнитная индукция 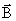 характеризует силовое действие магнитного поля на ток (аналогично,
характеризует силовое действие магнитного поля на ток (аналогично,  характеризует силовое действие электрического поля на заряд).
характеризует силовое действие электрического поля на заряд). 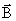 – силовая характеристика магнитного поля, ее можно изобразить с помощью магнитных силовых линий. Поскольку М – момент силы и
– силовая характеристика магнитного поля, ее можно изобразить с помощью магнитных силовых линий. Поскольку М – момент силы и  – магнитный момент являются характеристиками вращательного движения, то можно предположить, что магнитное поле – вихревое. Условились, за направление
– магнитный момент являются характеристиками вращательного движения, то можно предположить, что магнитное поле – вихревое. Условились, за направление 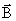 принимать направление северного конца магнитной стрелки. Силовые линии выходят из северного полюса, а входят, соответственно, в южный полюс магнита.
принимать направление северного конца магнитной стрелки. Силовые линии выходят из северного полюса, а входят, соответственно, в южный полюс магнита.
Как известно, электрический ток – упорядоченное движение зарядов, а, как мы доказали только что, магнитное поле порождается движущимися зарядами. Найдем магнитное поле, создаваемое одним движущимся зарядом (рис. 1.5).

В уравнении (1.2.2) заменим ток I на jS, где j – плотность тока. Векторы  и
и  имеют одинаковое направление, значит
имеют одинаковое направление, значит

Если все заряды одинаковы и имеют заряд q, то
 , ,
| (1.3.1) |
где n – число носителей заряда в единице объема;  – дрейфовая скорость зарядов.
– дрейфовая скорость зарядов.
Если заряды положительные, то  и
и  имеют одно направление (рис. 1.4). Подставив (1.3.1) в (1.2.2), получим:
имеют одно направление (рис. 1.4). Подставив (1.3.1) в (1.2.2), получим:
 , ,
| (1.3.2) |
Обозначим  – число носителей заряда в отрезке
– число носителей заряда в отрезке  . Разделив (1.3.2) на это число, получим выражение для индукции магнитного поля, создаваемого одним зарядом, движущимся со скоростью
. Разделив (1.3.2) на это число, получим выражение для индукции магнитного поля, создаваемого одним зарядом, движущимся со скоростью  :
:
 , ,
| (1.3.3) |
В скалярнойформе индукция магнитного поля одного заряда в вакууме определяется по формуле:
 , ,
| (1.3.4) |
Эта формула справедлива при скоростях заряженных частиц  .
.
Еще одной характеристикой магнитного поля является напряженность. Напряженностью магнитного поля называют векторную величину 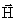 , характеризующую магнитное поле и определяемую следующим образом:
, характеризующую магнитное поле и определяемую следующим образом:
 , ,
| (1.4.1) |
Напряженность магнитного поля заряда q, движущегося в вакууме равна:
 , ,
| (1.4.2) |
Это выражение показывает закон Био–Савара–Лапласа для 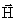 . Напряженность магнитного поля
. Напряженность магнитного поля 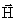 является, как бы, аналогом вектора электрического смещения
является, как бы, аналогом вектора электрического смещения  в электростатике.
в электростатике.
Применим закон Био–Савара–Лапласа для расчета магнитных полей простейших токов. Рассмотрим магнитное поле прямого тока (рис. 1.6).
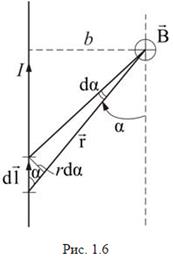
Все векторы  от произвольных элементарных участков
от произвольных элементарных участков  имеют одинаковое направление. Поэтому сложение векторов можно заменить сложением модулей. Пусть точка, в которой определяется магнитное поле, находится на расстоянии b от провода. Из рисунка 1.6 видно, что:
имеют одинаковое направление. Поэтому сложение векторов можно заменить сложением модулей. Пусть точка, в которой определяется магнитное поле, находится на расстоянии b от провода. Из рисунка 1.6 видно, что:

Подставив найденные значения r и d l в закон Био–Савара–Лапласа, получим:

Для конечного проводника угол α изменяется от  , до
, до  . Тогда
. Тогда
 , ,
| (1.5.1) |
Для бесконечно длинного проводника  а
а  , тогда
, тогда

или, что удобнее для расчетов,
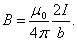 , ,
|
Рассмотрим поле, создаваемое током I, текущим по тонкому проводу, имеющему форму окружности радиуса R (рис. 1.7).

Определим магнитную индукцию на оси проводника с током на расстоянии х от плоскости кругового тока. Векторы  перпендикулярны плоскостям, проходящим через соответствующие
перпендикулярны плоскостям, проходящим через соответствующие  и
и  . Следовательно, они образуют симметричный конический веер. Из соображения симметрии видно, что результирующий вектор
. Следовательно, они образуют симметричный конический веер. Из соображения симметрии видно, что результирующий вектор 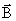 направлен вдоль оси кругового тока. Каждый из векторов
направлен вдоль оси кругового тока. Каждый из векторов  вносит вклад равный
вносит вклад равный 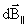 , а
, а  взаимно уничтожаются. Но
взаимно уничтожаются. Но 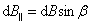 ,
,  , а т.к. угол между
, а т.к. угол между  и
и  α – прямой, то
α – прямой, то  тогда получим
тогда получим
 , ,
| (1.6.1) |
Подставив в (1.6.1)  и, проинтегрировав по всему контуру
и, проинтегрировав по всему контуру  , получим выражение для нахождения магнитной индукции круговоготока:
, получим выражение для нахождения магнитной индукции круговоготока:
 , ,
| (1.6.2) |
При  , получим магнитную индукцию в центре кругового тока:
, получим магнитную индукцию в центре кругового тока:
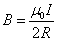 , ,
| (1.6.3) |
Заметим, что в числителе (1.6.2)  – магнитный момент контура. Тогда, на большом расстоянии от контура, при
– магнитный момент контура. Тогда, на большом расстоянии от контура, при  , магнитную индукцию можно рассчитать по формуле:
, магнитную индукцию можно рассчитать по формуле:
 , ,
| |

