Дифференциальные уравнения движения реальной жидкости.

Дифференциальные уравнения движения реальной (вязкой) жидкости можно получить дополнив уравнения Эйлера, выведенные для идеальной (невязкой) жидкости, составляющими сил внутреннего трения, обусловленными вязкостью.

Входящие в уравнение Эйлера объемные (массовые) силы, отнесенные к единице массы жидкости и определяемые поэтому через проекции соответствующих ускорений X, Y, Z и , , , останутся при этом неизменными, а силы поверхностные будут иными и кроме нормальных сил давления, выражаемых через нормальные напряжения, будут иметь место касательные (вязкостные) силы сопротивления, выражающиеся через соответствующие касательные напряжения.

Подобный вывод уравнений для нахождения составляющих сил сопротивления по координатным осям очень трудоёмок, рассмотрим упрощенное решение этой задачи, приводящее к тем же конечным результатам, что и точный вывод. Выделим в движущейся жидкости объем в форме элементарного параллелепипеда с гранями, параллельными координатным плоскостям, и сторонами dx, dy, dz. Сначала для простоты исследуем одноразмерные движения этого объема. Будем считать, что оно происходит вдоль оси х и скорость движения изменяется только в направлении оси z.

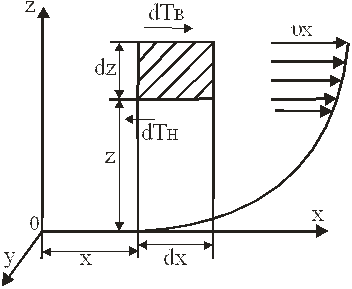
Представим себе далее, что твердая неподвижная поверхность, совпадает с плоскостью ХОУ, тормозит движение жидкости и значение скорости от нуля на этой поверхности возрастет по некоторой кривой.

При положительном градиенте скорости вдоль оси ОZ на горизонтальных гранях, ограничивающих выделенный параллелепипед, возникнут элементарные силы трения: на нижней грани направленная против движения, на верхней грани, где касательное напряжение получило приращение dxdy направленная в сторону движения.

Таким образом, равнодействующая указанных сил трения в направлении оси х будет

Подставим сюда значение напряжения внутреннего трения определяемое уравнением , (где 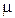-динамическая вязкость, которая для данной жидкости, находящейся в определенных условиях, может считаться постоянной).

Тогда

Отнесем затем это выражение к единице массы, т.е. разделим на dm=ρ dxdydz. Обозначим так же µ/ρ через υ (кинематическая вязкость), получим

.

Перейдем теперь к общему случаю трехмерного движения жидкости в пространстве, при котором существуют составляющие скорости в направлении всех трех координатных осей. Составляющие являются функциями трех координат по аналогии с частным случаем одномерного движения.

Аналогичные выражения смогут быть записаны для проекций единичной силы сопротивления на оси y и z.

Дополняя полученными выражениями (2) дифференциальные уравнения Эйлера, получаем дифференциальные уравнения движения реальной (вязкой) жидкости:

+

+

+

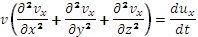
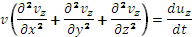
Впервые эти уравнения были получены в 1822 г. французским гидромехаником Навье, затем в 1845 г. их вывод был усовершенствован англичанином Стоксом. Поэтому их называют уравнениями Навье- Стокса.