Уравнение Бернулли

Уравнение Бернулли является основным в технической гидромеханике. Оно устанавливает зависимость между скоростью и давлением в различных точках движущейся жидкости. Рассмотрим уравнение Эйлера для движения невязкой жидкости:

;

;

.

Координатные оси расположим так, чтобы оси х и у были в горизонтальной плоскости, а ось z направлена вертикально вверх.

Приведем систему уравнений Эйлера к виду удобному для интегрирования. С этой целью умножим каждое из уравнений на соответствующие перемещения , , (проекции элемента траектории на соответствующие оси координат) и почленно сложим три уравнения, в результате чего получим

(1)

Первый трехчлен в условиях установившегося движения равен полному дифференциалу гидродинамического давления, отнесенному к плотности жидкости:

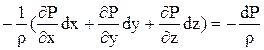
Рассмотрим движение жидкости только под действием силы тяжести, как наиболее распространенное на практике. Следует отметить, что жидкость под действием силы тяжести может двигаться в любом направлении в том числе и вертикально вверх.

Величины x, y, z выражают внешние массовые силы, заданные в виде проекций ускорений на соответствующие координатные оси. В рассматриваемом случае действует только сила тяжести, ускорение свободного падения которой равно g и тогда в принятых направлениях координатных осей можно записать

, , поэтому трехчлен

Правую часть уравнения (1) преобразуем, зная что, перемещения соответственно равны. , , к следующему виду:

,

где U- местная скорость в живом сечении струйки.

Подставим в уравнение (1) соответствующие значения трехчленов, запишем

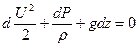или (2)

Если разделить все члены уравнения (2) на g получим уравнение отнесенной к единице веса:

После интегрирования запишем .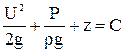

Это выражение было получено в 1738 г. академиком Российской Академии наук Д. Бернулли и называется уравнением Д. Бернулли для элементарной струйки установившегося движения невязкой жидкости.

Для вывода уравнения применительно к элементарной струйке вязкой жидкости рассмотрим его энергетический смысл.

Энергия, отнесенная к единице силы тяжести (веса жидкости) называется удельной энергией или напором. Уравнение Д. Бернулли математически выражает закон сохранения механической энергии, открытый Ломоносовым: вдоль элементарной струйки невязкой жидкости сумма потенциальной и кинетической энергии постоянная величина.

Сумма представляет собой часть удельной энергии- удельную потенциальную энергию, состоящую из удельной энергии положения z и удельной потенциальной энергии давления . Выражение называется удельной кинетической энергией. Вдоль элементарной струйки удельные потенциальная и кинетическая энергии могут изменяться, но их сумма остается постоянной.

При движении вязкой жидкости суммарная удельная энергия (потенциальная и кинетическая) движущейся жидкости вдоль струйки убывает в силу различных гидравлических сопротивлений. Следовательно, для элементарной струйки вязкой жидкости, находящейся в установившемся движении

Чтобы получить равенство правой и левой частей неравенства, необходимо в правой части добавить дополнительный член h, обозначающий затрату удельной энергии на преодоление сопротивлений при движении реальной (вязкой) жидкости в пределах между первым и вторым сечениями.

В этом случае уравнение Д. Бернулли принимает вид

.

Затрачиваемая на преодоления гидравлических сопротивлений часть энергии превращается из механической в тепловую, причем этот процесс необратим, соответствующий этой потере удельной энергии напор называют потерей напора.

Для характеристики относительного изменения полного напора на единицу длины струйки вводится понятие гидравлический уклон. Аналитически гидравлический уклон i представляет собой производную от потери напора по соответствующему расстоянию, отсчитанному от начального сечения по оси струйки.

.

Гидравлический уклон – отвлеченная безразмерная величина. Среднее значение гидравлического уклона на участке элементарной струйки между сечениями 1-1 и 2-2 определяется как потеря напора на единицу длины струйки:

,

где - расстояние между сечениями 1-1 и 2-2.