
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие гидродинамики.
|
|
Гидродинамикой называется раздел гидравлики, изучающий движение жидкости, а так же взаимодействие между жидкостью и твердыми телами при их относительном движении. Исходя из этого вводят понятие о внутренней и внешней задачах механики жидкости.
К внутренней задаче относиться движение жидкости в трубах, каналах и т.п., а к внешней задаче относиться обтекание потоком твердых тел.
В гидродинамике рассматриваются две модели жидкости: идеальные (или невязкие) и реальные (вязкие).
При изучении принимается, что жидкости являются сплошной средой даже при бесконечно малых объемах. Поэтому гидродинамику можно считать в общем случае разделом механики сплошных средств. В гидродинамике существуют два метода изучения движения жидкости. Метод Лагранжа и метод Эйлера.
Метод Лагранжа: заключается в изучении движения каждой отдельной частицы жидкости. В этом случае движение определяется положением частицы жидкости в функции от времени t. В начальный момент времени  ее положение определено начальными координатами
ее положение определено начальными координатами  . При движении частица перемещается в новую точку пространства с координатами
. При движении частица перемещается в новую точку пространства с координатами  и z. Движение частицы будет определено, если можно установить координаты х, у и z в заданной момент времени t в зависимости от начальных координат
и z. Движение частицы будет определено, если можно установить координаты х, у и z в заданной момент времени t в зависимости от начальных координат 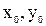 и
и  :
:


 .
.
Эта система уравнений дает возможность построить траекторию движения частицы жидкости и характеризует «историю» движения и ее «будущее». Величины х, у и z являются переменными Лагранжа, а их изменение за время  позволяет получить значения
позволяет получить значения  и затем путь
и затем путь  .
.
Проекция скорости на координатные оси определяются зависимостями  ,
,  ,
,  ,
,
а местная скорость  .
.
Таким образом, метод Лагранжа, сводиться к определению семейства траекторий движения частиц движущейся жидкости.
Метод Лагранжа в гидравлике не нашел широкого применения ввиду его относительной сложности.
Метод Эйлера: основан на изучении поля скоростей, под которым понимается вся система векторов, представляющих величину и направление скоростей в соответствующих точках пространства, занятого движущейся жидкостью в данный момент времени. Таким образом, поле скоростей представляет собой совокупность векторов местных скоростей. Построение поля скоростей в разных точках для разных моментов времени достаточно полно характеризует движение жидкости.
Переменными Эйлера являются значения скоростей 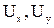 и
и  которые определяются в зависимости от координат точек пространства х, у, z и времени t:
которые определяются в зависимости от координат точек пространства х, у, z и времени t:


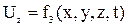
метод Эйлера нашел широкое применение в гидравлике. Он позволяет определить скорость в данной точке пространства в любой момент времени; скорость в данной точке пространства (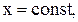

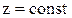 ) с течением времени; скорость t в фиксированный момент времени (
) с течением времени; скорость t в фиксированный момент времени ( в различных точках пространства.
в различных точках пространства.
В то же время метод Эйлера не позволяет изучить движение отдельной частицы жидкости. Следует добавить, что гидродинамическое давление p по аналогии, скоростью определяется как 
Основные понятия кинематики.
Кинематикой жидкости называется раздел гидродинамики, в котором рассматривают виды и формы движения жидкости без учета сил под действием которых происходит движение.
Жидкость состоит из бесконечно большого числа частиц, которые при рассмотрении уравнений движения физически представляются как очень малая масса жидкости, занимающая соответственно малый объем. В процесс движения жидкости изменяются во времени взаимные положения, ее частиц и их форма.
Деформируемость частицы жидкости является ее главной кинематической особенностью как элемента сплошной среды.
Под точкой пространства понимают геометрический образ, не имеющий размеров, положение которого в пространстве определяется тремя координатами х, у, z. Таким образом, через данную точку пространства проходят разные частицы жидкости, а положение движущейся жидкой частицы определяется координатами.
Частица жидкости при движении характеризуется плотностью, местной скоростью и гидродинамическим давлением.
Плотность жидкости  принимается постоянной.
принимается постоянной.
Местной скоростью называется скорость частицы жидкости в данной точке пространства, в данный момент времени t, то есть 
В проекциях на оси координат следует различать составляющие скорости  , тогда
, тогда  .
.
Полная производная каждой из составляющих скоростей может быть представлена в виде
 где
где  ,
,  ,
, 
проекции скорости на соответствующие оси, представляющая собой отношение проекции пути на соответствующие оси за время t.
Гидродинамическое давление Р характеризует давление в данной точке движущейся жидкости (аналогично гидростатическому давлению) и по аналогии с местной скоростью может быть записано как  . При движении частиц жидкости различают линию тока, элементарную струйку, вихревую линию и вихревую трубку.
. При движении частиц жидкости различают линию тока, элементарную струйку, вихревую линию и вихревую трубку.
Линией тока называется линия, касательная к каждой точке которой в данный момент времени совпадает с направлением вектора местной скорости. Следовательно, линия тока отражает мгновенную картину движения в различных точках. Так как путь частиц жидкости представляет траекторию ее движения с течением времени, то только в случае установившегося движения линии тока совпадает с траекториями движущихся частиц жидкости.

Поверхность, образованная линиями тока, проведенными через все точки бесконечно малого замкнутого контура, называется трубкой тока.
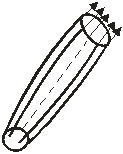
Масса жидкости, протекающей внутри трубки тока, называется элементарной струйкой. Таким образом, элементарную струйку можно рассматривать как движущийся бесконечно малый объем жидкости вокруг линии тока. В условиях установившегося движения элементарная струйка обладает такими свойствами: ее форма остается неизменной с течение времени, поверхность элементарной струйки является непроницаемой, то есть частицы жидкости не могут войти или выйти через нее; вследствие малости поперечного сечения струйки скорости во всех его точках принимаются одинаковыми и равными местной скорости.
Вихревая линия (е) - это линия, касательная во всех точках к векторам угловых скоростей частиц. Вихревая линия аналогична линии тока. Поверхность, ограниченная вихревыми линиями, проведенными через все точки какого-нибудь бесконечно малого простого замкнутого контура, находящегося в области движущейся жидкости, называется вихревой трубкой.
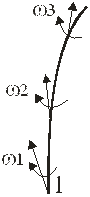
Вихревая трубка аналогична трубке тока. Массу движущейся жидкости внутри вихревой трубки называют вихревым шнуром. Вихревой шнур обладает такими свойствами: его сечение нигде не может быть равным нулю, так как в этом случае скорость вращения должна стать бесконечной, что физически не возможно; вихревые шнуры не могут заканчиваться или начинаться внутри жидкости- они либо замыкаются на себе, образуя вихревые кольца, либо опираются на плоскую стенку или свободную поверхность.


