Центр давления.

Центром давления называется точка приложения равнодействующей силы избыточного давления.

Рассмотрим произвольную плоскую фигуру, лежащую внутри жидкости в пределах боковой наклонной поверхности под углом α к горизонту. Выберем начало координат на свободной поверхности жидкости в месте ее пересечения с боковой стенкой, ось х считаем горизонтальной и направленной нормально к плоскости чертежа.

Для удобства рассмотрения мысленно совместим боковую стенку с плоскостью чертежа. Выделим в пределах рассматриваемой плоской фигуры произвольную точку А с координатой х, находящуюся на глубине h под свободной поверхностью жидкости и отстоящую от оси х на расстоянии .

Поскольку избыточное гидростатическое давление в рассматриваемой точке 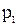, элементарная сила избыточного давления, действующая на элементарную площадку 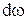, выделенную вокруг этой точки,

.

Элементарный момент этой силы относительно оси х

.

Тогда суммарный момент силы избыточного давления, действующей на рассматриваемую плоскую поверхность,

(2)

Из теоретической механики известно, что

, (3)

где 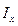- момент инерции плоской фигуры относительно оси х.

Но тот же момент силы

(1)

где 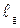- расстояние от оси х до точки приложения силы избыточного давления то есть искомая координата центра давления.

Сила избыточного давления

.

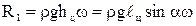Подставляя в (1) с учетом (2) и (3), получим

.

Откуда (5)

Момент инерции относительно горизонтальной оси, параллельной оси, проходящей через центр тяжести фигуры,

, (4)

где - момент инерции плоской фигуры относительно центральной оси.

Подставляя (4) в (5) получим

.

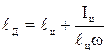Таким образом, центр давления лежит ниже центра тяжести плоской фигуры на величину

.

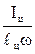Центр тяжести и центр давления могут совпадать только тогда, когда рассматриваемая плоская поверхность лежит в горизонтальной плоскости (в этом случае )

Зная силы 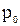и 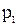и координаты точек приложения и , по правилу сложения параллельных сил нетрудно определить равнодействующую этих сил

, и точку приложения.

Моменты инерции для наиболее распространенных плоских фигур:

для квадрата со стороной а

;

для прямоугольника шириной В и высотой H

;

для круга диаметром d

.
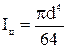