Потери напора при ламинарном режиме.

Зная закон распределения скоростей в поперечном сечении, можно без труда вывести теоретические формулы для определения расхода жидкости и потери напора на трение по длине потока при ламинарном режиме.

Для этого выделим в трубе элементарное сечение в виде кольца внутренним радиусом у, толщиной dy и, следовательно, площадь сечения .

Так как толщина кольца взята нами бесконечно малой, примем, что во всех его точках скорость частиц жидкости 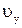одинакова и можно быть определена по уравнению

.

Элементарный расход жидкости, проходящий через это кольцевое сечение,

.

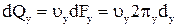Полный расход жидкости через все поперечное сечение трубы определяется как сумма таких элементарных расходов или, что то же самое, как интеграл, взятый по всему сечению, т.е. в пределах от у=0 до у=r.

Таким образом,

.

Интегрируя это выражение по частям, находим;

Первый член в правой части этого уравнения равен нулю, так как при у=r (у стенок) , а на оси трубы у=0. Следовательно

(1)

Введем сюда новую переменную 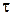. Из выражения имеем

(2)

Примем во внимание также

Тогда, поскольку , то (3)

Подставив в выражение (1) вместо у² и их значения (2) и (3) получим окончательно:

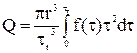(4)

Интегрирование этого выражения дает возможность получить необходимые для выполнения практических расчетов соотношения между расходом и перепадом давления при любом виде функции . Рассмотрим решение этой задачи для случая течения ньютоновской жидкости, когда .

Подставив это значение в уравнение (4) будет иметь:

.

Откуда после интегрирования найдем

или, что то же самое .

Производя замену , а также 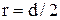(где d- диаметр трубы), получим окончательно формулу для определения расхода при ламинарном режиме:

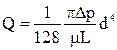, называемую формулой Гогена - Пуазейля.

При этом средняя скорость для всего сечения трубы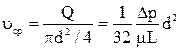

и, как это видно при сравнении с установленным ранее значением максимальной осевой скорости , будет равна половине этой скорости .

Из последней формулы легко найти искомую потерю напора

.

Последнее выражение несколько преобразуем, умножив числитель и знаменатель правой части на . Выполнив затем перегруппировку величин, получим:

.