Пульсация скорости и давления.

Наблюдения за скоростью и давлением в какой-либо точке турбулентного потока указывают на их колебания (пульсацию). Скорость изменяется по времени беспорядочно, не периодически, отклоняясь от некоторого устойчивого среднего положения.

Турбулентное движение, как отмечено выше является неустановившимся. Определенный порядок может быть наведен, если разделить переменную величину- мгновенную местную скорость на две части: - осредненную по времени и скорость пульсации (пульсационная добавка), которая может быть как со знаком плюс, так и со знаком минус.

В общем случае можно записать

где U _i -местная осредненная скорость, относящаяся к основному (первичному) движению; это скорость с которой водоворот (вихрь) увлекается общим течением мимо наблюдаля;

- скорость пульсации (пульсационная добавка или составляющая), относящаяся ко вторичному движению и отражающая колебание (пульсацию) скорости, то есть это схематически выдержанная относительная скорость внутри водоворота (вихря) в наблюдаемой точке пространства.

Для примера рассмотрим изменение во времени проекции скорости на ось Х, которая следуя общей закономерности также отклоняется от некоторого устойчивого значения , определяемого зависимостью

, (1)

где Т- время осреднения.

Время осреднения Т выбирается так, чтобы от него не зависела величина . По аналогии найдем и , а затем определим и осредненную местную скорость

.

Введя понятие местной осредненной скорости, турбулентное движение в области, на границах которой условия не изменяются с течение времени (при осреднении скорости), можно считать установившемся.

Отклонение мгновенной местной скорости от осредненной, как отмечено выше, называется пульсационной скоростью: .

Так как пульсация не ограниченна ни числовым значением, ни знаком, то в соответствии с (1) получим

.

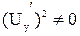Точно также , и , но в тоже время , и , так как при такой записи суммируются величины только со знаком плюс. В общем случае так же не равны нулю выражения , и ,

так как величины 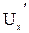, , 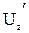разные так как по величине, так и по знаку.

Величины и позволяют понять характер турбулентности и произвести его анализ. Следует отметить, что при движении жидкости в трубах, прямолинейных руслах основное внимание уделяется изучению продольной составляющей, пульсации, так как поперечная и вертикальная 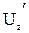значительно меньше.

В турбулентном потоке имеет место и пульсация гидродинамического давления p, осредненное значение которого .

Вводя понятие осредненных скорости и давления вместо реального турбулентного потока рассматривают его осредненную модель. Осредненная модель турбулентного потока нашла широкое применение в инженерной гидравлике. Для такой модели справедливы все результаты и зависимости, полученные раньше. Это относится к уравнениям Д. Бернулли и неразрывности движения, к распределению касательных напряжений при равномерном движении и т. п.

В частности, расход определяется с учетом закона распределения местной осредненной скорости по живому сечению ,

a соответствующая средняя в сечении скорость .