Потери напора при турбулентном режиме движения жидкости.

Знание закона распределения местных осредненных скоростей в плоскости живого сечения позволяет перейти к определению потерь на трение 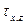, которые пропорциональны квадрату скорости при турбулентном режиме движения. При этом отношение удобно представить в долях скоростного напора :

,

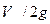где 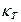- коэффициент пропорциональности.

Учитывая, что , можно записать: ,

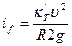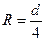или . Так как , а , то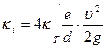

Заменяя значения 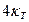через гидравлический коэффициент трения l, окончательно получим

Для определения коэффициента l при турбулентном режиме движения нет теоретических решений, поэтому он находится по эмпирическим формулам в зависимости от структуры турбулентного потока.

Экспериментальными исследованиями И. Никурадзе в Германии (1920-е годы) найдена и представлена зависимость , где относительная шероховатость .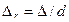

Результаты эксперимента представлены в виде графика Никурадзе.

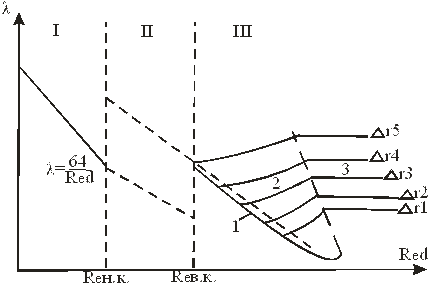
Он имеет следующие особенности. По горизонтальной оси расположены 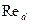в логарифмическом масштабе, чтобы охватить возможно больший диапазон значений 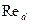, и в то же время достаточно детально представить области малых значений , относящихся к ламинарному режиму движения. На графике приведены кривые зависимости 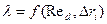для каждого фиксированного значения относительной шероховатости .

Зоны ламинарного (1), переходного (2) и турбулентного (3) режимов движения определяют вертикальные линии Re_н.к. и Re_в.к.. При ламинарном режиме движения не зависит от шероховатости и определяется как 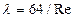, что совпадает с теоретическим выводом. На переходную зону (2) неустойчивого режима движения распространяются зависимости для , экстраполируя их из зоны турбулентного режима движения.

При турбулентном режиме движения (3) в его зоне различают три области (1, 2, 3).

В области 1 коэффициент не зависит от относительной шероховатости, и все линии, отвечающие различным значениям , сливаются в одну. Это область гидравлически гладких поверхностей, и для них коэффициент определяется по зависимости Блазиуса:

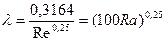
С учетом, что , и формулы Дарси, можно посчитать, что потери по длине в этой области пропорциональны скорости в степени 1, 75

,

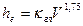где - коэффициент пропорциональности.

В области 3 коэффициент не зависит от числа Re, а зависит только от относительной шероховатости .

Здесь линии 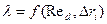, параллельны оси Re, это область гидравлически шероховатых поверхностей, и для них коэффициент определяется в зависимости от рода и состояния поверхности, например по формуле Л. Прандтля:

,

где 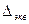- эквивалентная шероховатость, то есть такая равномерная шероховатость, которая дает при расчете одинаковую с заданной шероховатостью величину . Значения 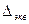приводятся в справочной литературе.

Учитывая, что в этом случае 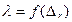, можно установить, что потери напора пропорциональны квадрату скорости:

,

где - коэффициент пропорциональности.

В связи с этим область 3 называют областью квадратичного или квадратического сопротивления гидравлически шероховатых поверхностей.

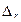В области 2 коэффициент зависит от Re и от и определяется по эмпирическим зависимостям, например, по формуле А.Д. Альтшуля:

В этой переходной области зависимость потерь напора в области может быть представлена в виде

В связи с этим переходную область 2 называют областью доквадратичного сопротивления гидравлически шероховатых поверхностей.

В соответствии с рекомендациями А. Д. Альтшуля, можно принять так же критерии для этих трех областей:

если 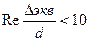- то это область гидравлически гладких труб;

если 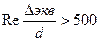, то это область квадратичного сопротивления гидравлически шероховатых труб;

если 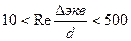, то это переходная область, или область доквадратичного сопротивления гидравлически шероховатых труб.

При турбулентном режиме для определения коэффициента в разное время было предложено большое число расчетных формул.

Для области гидравлически гладких труб можно применить формулу Конакова: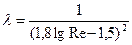

К указанной области сопротивления относятся технически гладкие трубы (из цветных металлов – медные, латунные, свинцовые, стеклянные трубы и др.) во всем диапазоне их практического использования по числам Re, а так же стальные трубы до значений числа Рейнольдса, ориентировочно равных 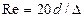(здесь 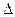- эквивалентная или абсолютная шероховатость).

В области гидравлически шероховатых труб (квадратичная область), значения можно получить по формуле Никурадзе

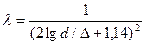
или близкой к ней формуле Шифринсона

.

Для старых водопроводных (стальных и чугунных) труб, значительно координированных в результате длительной эксплуатации ( мм) применимо так же выражение .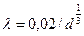

Близкие к опытным значениям результаты дает универсальная формула Альтшуля (применяемая во всех областях турбулентного режима)

.

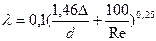Лекция 12. Местные гидравлические сопротивления. Коэффициент местных потерь. Местные потери при малых числах Рейнольдса. Переходная зона. Эквивалентная длина трубы. Принцип наложения потерь.