Задание № 3

Исследовать функцию и построить график

.

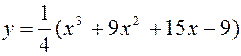Решение.

1) Областью определения данной функции являются все действительные значения аргумента х, то есть

D (y): 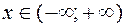а это значит, что функция непрерывна на всей числовой прямой и ее график не имеет вертикальных асимптот.

2) Исследуем функцию на интервалы монотонности и экстремумы. С этой целью найдем ее производную и приравняем нулю:

.

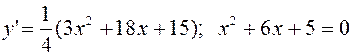Решая полученное квадратное уравнение, делаем вывод о том, что функция имеет две критические точки 1 рода х ₁ = - 5, х ₂ = - 1. Разбиваем область определения этими точками на части и по изменению знака производной в них выявляем промежутки монотонности и наличие экстремума:

х		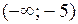-5	(-5, -1)	-1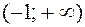
	+		—		+
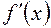
f (x)		max		min

.

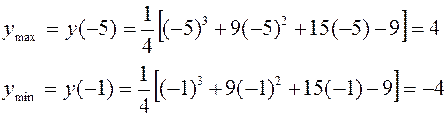3) Определим точки перегиба графика функции и интервалы его выпуклости и вогнутости. Для этого найдем вторую производную заданной функции и приравняем ее к нулю:

.

Итак, функция имеет одну критическую точку 2 рода
х = -3;. разобьем область определения полученной точкой на части, в каждой из которых установим знак второй производной:

x		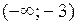-3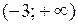
	—		+
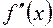
f (x)		т.п.

Значение х = - 3 является абсциссой точки перегиба графика функции, а ордината этой точки

.

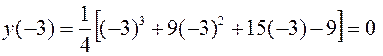4) Выясним наличие у графика заданной функции наклонных асимптот. Для определения параметров уравнения асимптоты

y = kx+b воспользуемся формулами

.

.

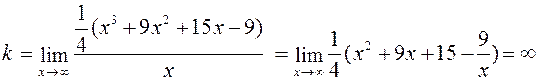Таким образом, у графика заданной функции наклонных асимптот нет.

5) Для построения графика изобразим точки максимума

А ₁(- 5; 4), минимума А ₂(- 1 - 4), перегиба А ₃(-3; 0) и точку

А ₄(0; 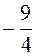). пересечения графика с осью Оу.

С учетом результатов предыдущих исследований построим кривую (см. рис. 1).

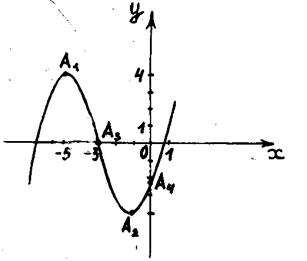
Рисунок 1 – Построение графика функции