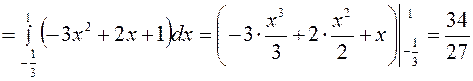Задание № 1. 1. Найти неопределенный интеграл

1. Найти неопределенный интеграл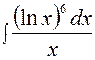

Решение. Применим подстановку 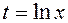, тогда 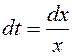и

;

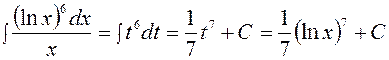2. Найти интеграл .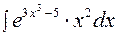

Решение. Применим подставку t =3 x ³ – 5.

Тогда 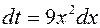; 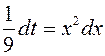, откуда

.

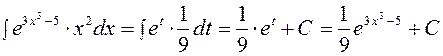Задание № 2

Найти интеграл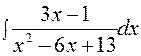

Решение. Преобразуем знаменатель дроби, стоящей под знаком интеграла следующим образом:

x ² – 6 x +13 = x ² – 6 x + 9 + 4 = (x - 3)² + 2². Тогда после подстановки t = x - 3 получаем

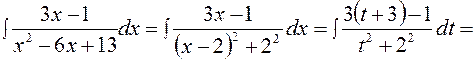
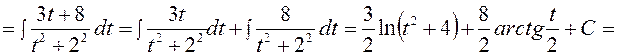
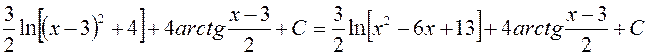причем, при вычислении интеграла 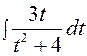воспользуемся заменой переменной z = t ²+4, тогда dz = 2 tdt, откуда

.

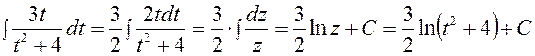Итак, учитывая, что t = x – 3, имеем

.

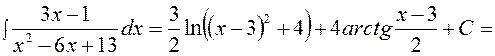
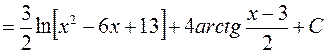Задание № 3

1. Найти интеграл .

Решение. Применим формулу интегрирования по частям

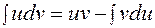
Положим

u = 3 x +7, dv = cos5 xdx,

тогда

du = 3 dx, .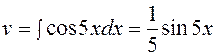

Следовательно,

.

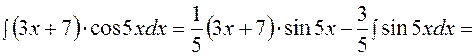
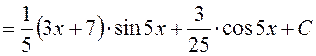2. Найти интеграл .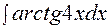

Решение.

Положим

u = arctg 4 x, dv = dx,

тогда

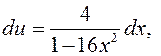v = x.

Отсюда

.

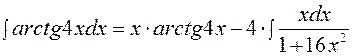Применяя в последнем интеграле подстановку t = 1+16 x ²,

получаем, 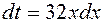, следовательно,

.

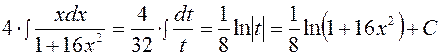Отсюда .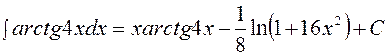

Задание № 4

Вычислить площадь, ограниченную параболами

y = 2 x ² – x – 2,

y = - x ² + x – 1.

Решение.

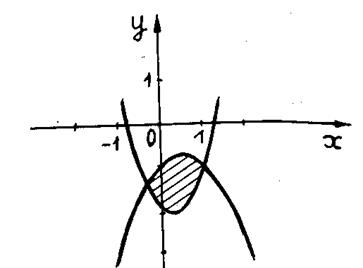
Рисунок 2 – График построения парабол

Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений:

2 x ² – x – 2 = - x ² + x – 1. Отсюда 3 x ² – 2 x – 1 = 0, D = 4 + 4∙ 3 = 16,

,

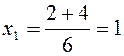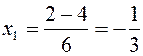
Вычисление площади осуществляем по формуле:

,

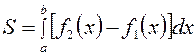где f ₁(x), f ₂(x) – кривые, ограничивающие фигуру (f ₂(x) ³ f ₁(x)).

В нашем случае