
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основное логарифмическое тождество
|
|
ФОРМУЛЫ
СОКРАЩЕННОГО УМНОЖЕНИЯ
РАЗНОСТЬ КВАДРАТОВ

| |
КВАДРАТ СУММЫ
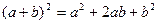
|
КВАДРАТ РАЗНОСТИ

|
СУММА КУБОВ

|
РАЗНОСТЬ КУБОВ

|
КУБ СУММЫ
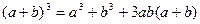
|
КУБ РАЗНОСТИ

|
СВОЙСТВА ЛОГАРИФМОВ
Определение. Логарифмом числа х по основанию а называется показатель степени, в которую надо возвести а, чтобы получить х, то есть:
log ax = b Û ab = x, если а > 0, а  1, х > 0
1, х > 0
Основное логарифмическое тождество
а log ax = х, если а > 0, а  1, х > 0
1, х > 0
Свойства логарифмов (х > 0;, у > 0; а > 0, а  1)
1)
1. log ax у = log ax + log aу
2. log  = log ax - log aу
= log ax - log aу
3. log ax к = к logа х
Формула перехода к логарифму по новому основанию

Следствия 1. 
2. 
3. 
Т Р И Г О Н О М Е Т Р И Я
Алгебраические соотношения между тригонометрическими функциями одного и того же аргумента
sin 2x + cos 2x = 1 tgx ctg x = 1
1 + tg 2 x =  1 + ctg 2 x =
1 + ctg 2 x = 
Формулы сложения аргументов
sin (х + у) = sin х cos у + cos х sin у
sin (х - у) = sin х cos у - cos х sin у
cos (х - у) = cos х cos у + sin х sin у
cos (х + у) = cos х cos у - sin х sin у
Формулы двойного аргумента
cos 2х = cos 2х - sin 2х
sin 2х = 2 sin х cos х
tg 2x = 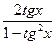
Следствие из формул двойного аргумента
1 + cos 2х = 2 cos 2х
1 - cos 2х = 2 sin 2х
Решение тригонометрических уравнений
sin x = а Û х = (-1)karcsin a +  k или
k или  k Î Z
k Î Z
cos x = а Û x =  arccos a + 2
arccos a + 2  k k Î Z
k k Î Z
tg x = a Û x = arctg a +  k k Î Z
k k Î Z
Частные виды тригонометрических уравнений
sin x = 0
х =  k k
| sin x = 1
х =  + 2 + 2  k k
| sin x = -1
x = -  + 2 + 2  k k
|
cos x = 0
х =  + +  k k
| cos x = 1
х = 2  k k
| Сos x = -1
x =  + 2 + 2  k k
|
Свойства обратных тригонометрических функций
| arсsin (-a ) = - arсsin a |
arccos (-a ) =  - arccos a - arccos a
|
| arctg (-a ) = - arctg a |
arcсtg (-a ) =  - arсctg a - arсctg a
|
Значения тригонометрических функций некоторых углов

| 
| 
| 
| 
| 
| 
| 
| 
| 
| ||
| sin | 
| 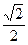
| 
| 
| 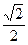
| 
| -1 | ||||
| cos | 
| 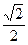
| 
| - 
| - 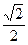
| - 
| -1 | ||||
| tg | 
| 
| Не $ | - 
| -1 | - 
| Не $ | ||||
| сtg | Не $ | 
| 
| - 
| -1 | - 
| Не $ | Не $ |
