
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема 1
|
|
. 



Теорема 2.

Алгоритм решения иррациональных уравнений:
Для того, чтобы не нарушить равносильность при возведении в квадрат обеих частей уравнения с квадратными корнями необходимо:
· Потребовать, чтобы все выражения, стоящие под знаком квадратного корня были неотрицательными.
· При возведении обеих частей в квадрат надо потребовать, чтобы обе части уравнения были неотрицательны
· Решить смешанную систему, состоящую из уравнения и неравенств
Показательные уравнения
Теорема 3.

Логарифмические уравнения
Теорема 4.

Замечания.
Если основание логарифма постоянное число, то первые две строчки в системе не записывают
Если в уравнении было несколько логарифмом, которые заменены одним, то в системе указываем, что каждое выражение, находившееся в исходном уравнении под знаком логарифма должно быть строго больше нуля
ПЛАНИМЕТРИЯ
ПЛОЩАДИ ТРЕУГОЛЬНИКОВ И МНОГОУГОЛЬНИКОВ
ТЕОРЕМА Площадь треугольника равна половине произведения высоты на основание.
 Если
Если  , и , и  , то , то 
|
СЛЕДСТВИЕ. Если  и и  - две высоты, то - две высоты, то 

|
ТЕОРЕМА. Площадь треугольника вычисляется по формуле  , где , где  , а, в, с – стороны треугольника, а r – радиус вписанной в треугольник окружности , а, в, с – стороны треугольника, а r – радиус вписанной в треугольник окружности

| ТЕОРЕМА. Площадь треугольника вычисляется по формуле  , где а, в, с – стороны треугольника, а R – радиус описанной около треугольника окружности , где а, в, с – стороны треугольника, а R – радиус описанной около треугольника окружности

|
ТЕОРЕМА Площадь треугольника равна половине произведения его сторон на синус угла между ними.

|
ТЕОРЕМА(ФОРМУЛА ГЕРОНА) Площадь треугольника со сторонами а, в, с вычисляется по формуле  , где , где 
 
|
ТЕОРЕМА Площадь прямоугольника равна произведению его высоты на основание, то есть произведению его сторон

|
ТЕОРЕМА Площадь параллелограмма (в частности, ромба) равна произведению его высоты на основание.

|
ТЕОРЕМА Площадь параллелограмма равна произведению его сторон на синус угла между ними.

| ТЕОРЕМА Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними (теорема верна для любого выпуклого четырехугольника).

|
ТЕОРЕМА Площадь ромба равна половине произведения диагоналей.
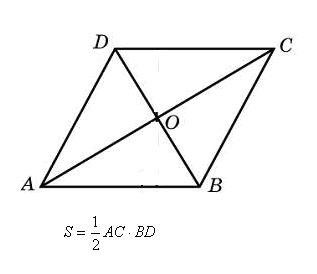
|
ТЕОРЕМА Площадь трапеции равна произведению полусуммы его оснований на высоту, или произведению его средней линии на высоту.

|
ТЕОРЕМА ВАРИНЬОНА Четырёхугольник, вершины которого совпадают с серединами сторон произвольного четырёхугольника, является параллелограммом, площадь которого равна половине площади исходного четырехугольника.
ТЕОРЕМА. Сумма углов четырехугольника. равна 360º
ТЕОРЕМА Средняя линия треугольника параллельна основанию и равна его половине. 
ТЕОРЕМА Площади подобных треугольников относятся как квадраты сходственных сторон.
СЛЕДСТВИЕ: Средняя линия отсекает от треугольника треугольник, площадь которого равна  площади исходного треугольника
площади исходного треугольника
ТЕОРЕМА Периметры подобных треугольников относятся как сходственные стороны.
СВОЙСТВА ВПИСАННЫХ И ОПИСАННЫХ ЧЕТЫРЕХУГОЛЬНИКОВ
ТЕОРЕМА В выпуклом вписанном четырехугольнике суммы противолежащих углов равны между собой и равны 180°.
ТЕОРЕМА Если в четырехугольник вписана окружность, то суммы противолежащих сторон его равны.