Равномерное движение в призматических и цилиндрических напорных трубах

Диаметр, поперечное сечение труб и расход жидкости постоянны Q, d, w = const: 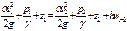. Пускай l - длина трубопровода, тогда: , где i_e - гидравлический уклон, i_f - уклон трения, так как v₁ = v₂, то , где i_p - пьезометрический уклон. При равномерном движении в напорных трубах три уклона равны: i_e = i_f = i_p.

Если р - гидродинамическое давление, a - угол наклона трубопровода к горизонту, Р₁ и Р₂ - нормальные сжимающие силы давления жидкости (горизонтальны и противоположнонаправлены), Т - паралельная дну составляющая вектора веса жидкости, F - сила трения (не зависящая от давления), то: P₁ - P₂ + T - F = 0; P₁ = p₁ × w; P₂ = p₂ × w; T = G × sin a = G × (z₁-z₂) / l = g × w × (z₁-z₂); F = t × c × l = 2 × t × l × Ö (pw), где t - касательное напряжение и c - длина смоченного периметра; подставляя в условие равновесия получим: p₁ × w - p₂ × w + g × w × (z₁-z₂) - 2 × t × l × Ö (pw) = 0; p₁ / g - p₂ / g + z₁-z₂ = t × c × l / g × w; пьезометрический уклон: i_p = (p₁ / g - p₂ / g + z₁-z₂) / l = t × c / g × w; так как w/c = R - гидравлический радиус, то i_p = t / g × R = i_f, если t = K_f × v², то получим формулу Шези: 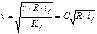, где - скоростной множитель, а n - коэффициент шероховатости.

Шероховатость - неровность твердой поверхности, влияющая на возникновение сил трения потока о стенки русла. Обозначив С × Ö R = W - скоростная характеристика: v = W × Ö i_f; тогда Q = w × W = K × Ö i_f, где К - расходная характеристика. Исходя из третьей водопроводной формулы: S = H/lQ² = i_f × l/l × i_f × K² = 1/K².