СДНФ функций алгебры логики.

Совершенная дизъюнктивная нормальная форма (СДНФ) — это такая ДНФ, которая удовлетворяет трём условиям:

в ней нет одинаковых элементарных конъюнкций

в каждой конъюнкции нет одинаковых пропозициональных букв

каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причём в одинаковом порядке.

Любая булева формула, не являющаяся тождественно ложной, может быть приведена к СДНФ, причем единственным образом, то есть для любой выполнимой функции алгебры логики существует своя СДНФ, причём единственная.

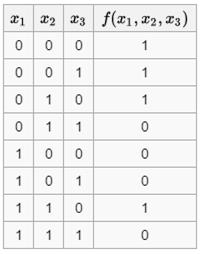
В ячейках результата отмечаются лишь те комбинации, которые приводят логическое выражение в состояние единицы. Далее рассматриваются значения переменных при которых функция равна 1. Если значение переменной равно 0, то она записывается с инверсией. Если значение переменной равно 1, то без инверсии.

Первая строка содержит 1 в указанном поле. Отмечаются значения всех трёх переменных, это:

Нулевые значения — тут все переменные представлены нулями — записываются в конечном выражении инверсией этой переменной. Первый член СДНФ рассматриваемой функции выглядит так:

Переменные второго члена:

в этом случае будет представлен без инверсии:

Таким образом анализируются все ячейки . Совершенная ДНФ этой функции будет дизъюнкцией всех полученных членов (элементарных конъюнкций).

Совершенная ДНФ этой функции:

33. СКНФ функций алгебры логики.

Совершенная конъюнктивная нормальная форма (СКНФ) — это такая КНФ, которая удовлетворяет трём условиям:

в ней нет одинаковых элементарных дизъюнкций

в каждой дизъюнкции нет одинаковых пропозициональных переменных

каждая элементарная дизъюнкция содержит каждую пропозициональную букву из входящих в данную КНФ пропозициональных букв.

Любая булева формула, не являющаяся тождественно истинной, может быть приведена к СКНФ.

В ячейках строки отмечаются лишь те комбинации, которые приводят логическое выражение в состояние нуля.

Четвёртая строка содержит 0 в указанном поле. Отмечаются значения всех четырёх переменных, это:

В дизъюнкцию записывается переменная без инверсии, если она в наборе равна 0, и с инверсией, если она равна 1. Первый член СКНФ рассматриваемой функции выглядит так: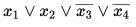

Остальные члены СКНФ составляются по аналогии.