
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лекция. Понятие первообразной, приложения первообразной
|
|
Понятие первообразной вводится в школе посредством задачи, для решения которой необходимо по известной производной найти (восстановить) саму функцию. Приведём пример такой задачи: «По прямой движется материальная точка, скорость которой в момент времени t задаётся формулой v = gt. Найти закон движения». Используя геометрический смысл производной, для решения задачи следует подобрать функцию, производная которой равна gt. Нетрудно догадаться, что  Действительно,
Действительно, 
Вводим определение: функцию  называют первообразной для функции
называют первообразной для функции  на заданном промежутке Х, если для любого
на заданном промежутке Х, если для любого  выполняется равенство
выполняется равенство 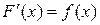 .
.
Пример 1.  ,
, 
 .
.
Пример 2.  ,
,  ,
, 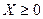 .
.
Контрпример.  не является первообразной для функции
не является первообразной для функции  на промежутке
на промежутке  , так как равенство
, так как равенство 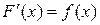 не выполняется при х = 0. Однако на каждом из промежутков
не выполняется при х = 0. Однако на каждом из промежутков  и
и  функция
функция  является первообразной для функции f.
является первообразной для функции f.
Для усвоения определения школьникам предлагаются задачи, в которых следует доказать, что некоторая функция F является или не является первообразной для функции f на заданном числовом множестве Х, то есть проверить равенство 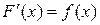 для всех х Î Х. Формулировка таких заданий может начинаться со слов: «угадайте первообразную функцию».
для всех х Î Х. Формулировка таких заданий может начинаться со слов: «угадайте первообразную функцию».
Когда у учащихся появляется первый опыт работы с понятием первообразной, они изучают теорему об основном свойстве первообразной. Для её доказательства рассматривается лемма (признак постоянства функции): если в каждой точке некоторого промежутка Х, функция f имеет равную нулю производную, то f – постоянна на этом промежутке.
Дано: функция  , Х – числовой промежуток.
, Х – числовой промежуток.
 при
при 
Доказать: 
Что ж это за функция, касательная к графику которой в любой точке параллельна оси Ох? Ясно, что её график – прямая, параллельная оси Ох, то есть функция имеет вид 
Приведём доказательство леммы по учебнику Колмогорова.
Доказательство
Зафиксируем некоторое значение х 0 из промежутка Х. Тогда для любого  по теореме Лагранжа найдётся такое число с, заключённое между х и х 0, что
по теореме Лагранжа найдётся такое число с, заключённое между х и х 0, что  Так как по условию
Так как по условию  при
при  , то
, то 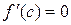 , следовательно,
, следовательно, 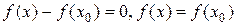 при всех
при всех  , то есть функция f сохраняет постоянное значение.
, то есть функция f сохраняет постоянное значение.
Приведённая лемма имеет богатые алгебраические приложения. Приведём один скромный пример.
Доказать тождество 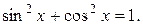
Пусть  . Найдём производную функции f.
. Найдём производную функции f.

 , следовательно,
, следовательно,  . Определим с. Пусть х = 0.
. Определим с. Пусть х = 0.  , что и требовалось доказать.
, что и требовалось доказать.
Сформулируем основное свойство первообразной.
Теорема. Любая первообразная для функции f на промежутке Х может быть записана в виде F (x) + c, где F (x) – одна из первообразных для функции f, а с – произвольная постоянная.
В теореме можно выделить два утверждения:
1) если F (x) – одна из первообразных для функции f, то функция F (x) + c также её первообразная.
Доказательство очевидно. Вывод: первообразная функции f определяется неоднозначно.
2) любая первообразная  функции f имеет вид F (x) + c.
функции f имеет вид F (x) + c.
Доказательство
 (по лемме):
(по лемме):
 .
.
Геометрический смысл: графики любых двух первообразных получаются друг из друга параллельным переносом вдоль оси Оу.

Далее совместно с учащимися составляем таблицупервообразных.
| Функция у = f (x) | хп, пÎ Z, п ¹ -1 | 
| sinx | cosx | 
| 
| ||
| Первообразная у = F (x) | C | x+c |  + c + c
|  +c +c
| - cosx+c | sinx+c | tg x+c | ctg x+c |
В дальнейшем таблица дополняется первообразными показательной и логарифмической функции.
Кроме таблицы первообразных, учащимся сообщаются 3 правила нахождения первообразных.
Правило1.Если F есть первообразная для f, а G - первообразная для g,
то F + G есть первообразная для f + g.
Правило2.Если F есть первообразная для f, а k -постоянная, то kF – первообразная для kf.
Правило3.Если F есть первообразная для f, а k и b -постоянные, причём
k¹ 0, то  – первообразная для – первообразная для 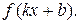
|
Все 3 правила легко доказываются по определению первообразной. Особое внимание следует уделить записи  в правиле 3. Следует обсудить с учащимися её смысл. Так, 1) если
в правиле 3. Следует обсудить с учащимися её смысл. Так, 1) если  , то
, то  ; 2) если
; 2) если 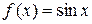 , то
, то  Согласно правилу 3 в здании (1) первообразная функции f равна
Согласно правилу 3 в здании (1) первообразная функции f равна  , а функции
, а функции  равна
равна  , а в здании (2)
, а в здании (2) 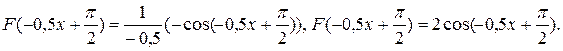
Первоначально полезно оформлять задания на нахождение первообразной в виде таблицы.
Пример. Найти общий вид первообразных для функции 
Решение

| 
| Обоснование |
 7
7  7
7 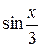
|  -7
-7  -7× 3
-7× 3 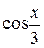 = -21 = -21 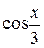
| Таблица Правило 2 Правило 3 |



| 

 = = 
| Таблица Правило 2 Правило 3 |



|  5×
5×  = = 

| Таблица Правило 2 Правило 3 |
Применяя правило 1, получаем ответ: F (x) = -21 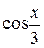 +
+  +
+ 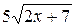 + c.
+ c.