
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теория алгоритмов
|
|
Неформально понятие алгоритма, как последовательности действий направленных на решение некоторой задачи, вводилось ещё в курсе информатики. Далее в курсах технологии программирования, дискретной математики, математической логики рассматривались алгоритмы решения различных типов задач. В данном разделе мы формализуем понятие алгоритма, введём понятие вычислительной сложности алгоритма, классифицируем алгоритмы.
Вид формальной модели алгоритма зависит от тех понятий, которые положены в основание модели.
1) Первый подход основан на представлении об алгоритме, как о программе для некоторого детерминированного устройства. К моделям этого типа относятся машины Тьюринга, канонические системы Поста, нормальные алгорифмы Маркова.
2) Второй подход основан на понятии вычисления и числовой функции, основная теоретическая модель этого вида – рекурсивные функции.
Перед введением формальных определений алгоритма сформулируем понятия, необходимые для дальнейшего изложения.
Всюду далее будет рассматриваться некоторая массовая задача P. Массовая задача P определяется следующей информацией:
1) общим списком параметров задачи;
2) формулировкой свойств, которым должно удовлетворять её решение.
Напомним, что этот набор называют ещё спецификацией задачи.
Индивидуальная задача I получается подстановкой в массовую задачу P данного вида конкретных значений параметров. Будем говорить, что алгоритм решает массовую задачу P, если применим к произвольной индивидуальной задаче I, соответствующей задаче P, и даёт решение задачи I.
В качестве массовой задачи P будем рассматривать задачу распознавания, т.е. задачу решением которой могут быть ответы “да” или “нет”. Например, задачей распознавания является задача определения – делится ли заданное натуральное число нацело на 4. Это не ограничивает общности, так как любая задача может быть сформулирована в терминах задачи распознавания.
Обозначим через
 – множество всех индивидуальных задач, соответствующих задаче P,
– множество всех индивидуальных задач, соответствующих задаче P,
 – множество индивидуальных задач с ответом “да”.
– множество индивидуальных задач с ответом “да”.
Таким образом, задача распознавания состоит в определении этих двух множеств.
Для записи задачи распознавания используется естественный формальный эквивалент, называемый языком. Обозначим
S – конечное множество символов (алфавит),
S* – множество всех конечных цепочек, составленных из S (слова),
 – подмножество S*, называемое языком.
– подмножество S*, называемое языком.
Соответствие между задачами распознавания и языками устанавливается с помощью схем кодирования. Схема кодирования e записывает каждую индивидуальную задачу из P словом в фиксированном алфавите S.
Множество S* делится задачей P и схемой кодирования e на 3 класса:
1) слова, не являющиеся кодами индивидуальных задач из P;
2) слова, являющиеся кодами с отрицательным ответом;
3) слова, являющиеся кодами с положительным ответом.
Третий класс слов обозначим  .
.

- Машины Тьюринга
Одноленточная детерминированная машина Тьюринга (ДМТ) представляет собой логическое устройство, которое состоит из:
1) неограниченной в обе стороны ленты, разделенной на одинаковые пронумерованные ячейки;
2) читающей/пишущей головки;
3) управляющего устройства с конечным числом состояний.
Схематически ДМТ можно представить в виде рисунка


Программу  для ДМТ определяют следующие компоненты:
для ДМТ определяют следующие компоненты:
1) G – конечное множество символов, записываемых на ленте,  – множество входных символов,
– множество входных символов,  – выделенный пустой символ;
– выделенный пустой символ;
2) Q – конечное множество состояний, в котором выделено начальное состояние  и два конечных –
и два конечных –  ;
;
3) функция переходов  .
.
Т.е.  .
.
Порядок работы ДМТ под управлением программы  .
.
1. Входное слово  записывается на ленте в ячейках с номерами
записывается на ленте в ячейках с номерами  (
( – длина слова x), все другие ячейки содержат пустой символ. Управляющее устройство находится в состоянии
– длина слова x), все другие ячейки содержат пустой символ. Управляющее устройство находится в состоянии  , а читающая/пишущая головка – над ячейкой с номером 1.
, а читающая/пишущая головка – над ячейкой с номером 1.
2. Если текущее состояние q не совпадает с одним из конечных состояний, то машина переходит в следующее состояние, определяемое согласно функции переходов. Пусть  , где s – считанный головкой символ из текущей ячейки. Тогда управляющее устройство переходит в состояние
, где s – считанный головкой символ из текущей ячейки. Тогда управляющее устройство переходит в состояние 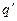 , головка вместо символа s записывает символ
, головка вместо символа s записывает символ  и сдвигается на одну ячейку влево, если
и сдвигается на одну ячейку влево, если  , или вправо, если
, или вправо, если  . Затем, текущим становится состояние
. Затем, текущим становится состояние 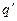 .
.
3. Если 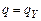 , то вычисления заканчиваются с результатом “да”, если
, то вычисления заканчиваются с результатом “да”, если  , то – с результатом “нет”.
, то – с результатом “нет”.
В качестве примера рассмотрим упоминавшуюся выше задачу распознавания “делимость на 4”. Построим ДМТ-программу  для решения этой задачи.
для решения этой задачи.
Для представления чисел будем использовать символы 0 и 1, а в качестве схемы кодирования – двоичную запись числа. Значит,  ,
,  .
.
Опишем словесно действия ДМТ, а затем формализуем в виде программы  . Число делится нацело на 4, если два последних символа в его двоичном представлении являются нулями. Поэтому, вначале машина будет считывать, повторять все символы входного слова и двигаться вправо, пока не дойдёт до пустого символа. После чего будет выполняться движение влево и анализ последнего и предпоследнего символа с последующей заменой его на символ b. Если хотя бы один из этих символов не равен 0, то результирующее состояние –
. Число делится нацело на 4, если два последних символа в его двоичном представлении являются нулями. Поэтому, вначале машина будет считывать, повторять все символы входного слова и двигаться вправо, пока не дойдёт до пустого символа. После чего будет выполняться движение влево и анализ последнего и предпоследнего символа с последующей заменой его на символ b. Если хотя бы один из этих символов не равен 0, то результирующее состояние –  , в противном случае –
, в противном случае –  . При любом конечном состоянии результатом на ленте будет частное от целочисленного деления, причём, если
. При любом конечном состоянии результатом на ленте будет частное от целочисленного деления, причём, если  , то им является пустое слово, т.е. 0.
, то им является пустое слово, т.е. 0.
Представим функцию переходов наглядно в виде ориентированного графа. Вершинами графа будут являться состояния управляющего устройства, дуги графа означают переход из одного состояния в другое, причём, над каждой дугой будем писать символ(ы), по которому выполняется переход, а после знака ® – замещающий символ(ы) и направление движения головки.
Следовательно,  .
.

Функцию переходов d можно также задать табличным способом.
| q | s | ||
| b | |||
| q 0 | (q 0, 0, 1) | (q 0, 1, 1) | (q 1, b, -1) |
| q 1 | (q 2, b, -1) | (q 3, b, -1) | (qN, b, -1) |
| q 2 | (qY, b, -1) | (qN, b, -1) | (qN, b, -1) |
| q 3 | (qN, b, -1) | (qN, b, -1) | (qN, b, -1) |
Программа  , имеющая входной алфавит S, принимает слово
, имеющая входной алфавит S, принимает слово  в том и только том случае, когда, будучи применённой ко входу x, она останавливается в состоянии
в том и только том случае, когда, будучи применённой ко входу x, она останавливается в состоянии  . Язык
. Язык  , распознаваемый программой
, распознаваемый программой  , определяется следующим образом
, определяется следующим образом
 .
.
Если  , то работа программы
, то работа программы  может либо завершиться в состоянии
может либо завершиться в состоянии  , либо бесконечно продолжаться без остановки. Будем говорить, что ДМТ-программа
, либо бесконечно продолжаться без остановки. Будем говорить, что ДМТ-программа  решает задачу распознавания P при схеме кодирования e, если
решает задачу распознавания P при схеме кодирования e, если  останавливается для любых
останавливается для любых  и
и 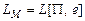 .
.
Работу ДМТ-программы  можно рассматривать, как вычисление некоторой функции
можно рассматривать, как вычисление некоторой функции  . Если слово
. Если слово  и программа
и программа  останавливается на любом входе из S*, то результатом вычисления
останавливается на любом входе из S*, то результатом вычисления  будет слово, составленное из символов, записанных на ленте после остановки машины в ячейках с 1-ой по последнюю непустую ячейку.
будет слово, составленное из символов, записанных на ленте после остановки машины в ячейках с 1-ой по последнюю непустую ячейку.
Функция  называется вычислимой (по Тьюрингу), если существует вычисляющий её алгоритм, т.е. $ программа
называется вычислимой (по Тьюрингу), если существует вычисляющий её алгоритм, т.е. $ программа  , такая что
, такая что  .
.
Свойства вычислимых функций.
1. Суперпозиция 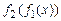 вычислимых функций
вычислимых функций  вычислима.
вычислима.
2. Любая вычислимая функция вычислима на машине Тьюринга с правой полулентой.
3. Если функции  вычислимы, то разветвление
вычислимы, то разветвление  также вычислимо.
также вычислимо.
Выше мы каждому алгоритму поставили в соответствие функцию. Является ли верным обратное утверждение: можно ли для произвольной функции построить алгоритм её вычисляющий? Ответ на этот вопрос отрицательный, т.е. произвольная функция не является вычислимой. Выделим класс функций, для которых вычисляющий их алгоритм существует, таким образом, мы дадим другое определение алгоритма в терминах функций.