Отношение эквивалентности в ИВ

Определим эквивалентность формул в исчислении высказываний.

Определение 1. Формулы U и B называются эквивалентными, что обозначается |- , если

|- (1)

Рассмотрим некоторые простые свойства отношения эквивалентности.

1. Рефлексивность: |- .

2. Симметричность: если |- 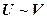, то |- .

3. Транзитивность: если |- 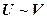и |- , то |- .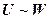

Задание 1. Доказать свойство симметричности отношения эквивалентности.

Решение.

1. |-

2. |-

3. |-

Из свойств отношения эквивалентности следует, что множество формул исчисления высказываний разбивается на непересекающиеся классы эквивалентных друг другу формул (классы эквивалентности). Следовательно, все теоремы исчисления высказываний образуют один класс эквивалентных формул.

В исчислении высказываний имеют место следующие эквивалентности, которые соответствуют аналогичным свойствам отношения эквивалентности алгебры высказываний.

1. |- .

2. |-

3. |-

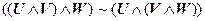
4. |-

5. |-

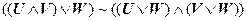
6. |-

7. |-

8. |-

9. |-

10. |-

11. |-

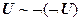
12. |-

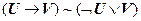
Для того чтобы доказать эквивалентность |- в исчислении высказываний достаточно построить выводы 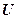|- 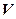и 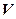|- 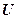. Покажем, что есл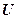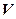и |- и |- 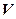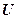, то |- .

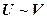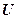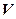
1. |-	по условию
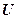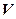
2. |-	по условию
3. |-	5 (1)
4. |-	5 (2)
5. , |-
6. |-	4 (3, 4, 5)

Последняя формула, в силу определения, означает ú - .

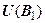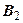Теорема эквивалентности. Если и - формулы, полученные заменой некоторых (одних и тех же) вхождений какой-либо высказывательной переменной в формуле U соответственно формулами и , то

|- .

Следствие. Если есть некоторая подформула формулы U и эквивалентна формуле 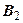, то формула, полученная заменой в формуле U на 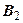, эквивалентна U. Иными словами, если , то .

Свойства 2, 4, 10 и теорема эквивалентности позволяют формулу, составленную из высказывательных переменных 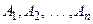лишь с помощью операции дизъюнкции, преобразовать к виду

.

Аналогично формула, составленная из с помощью операции конъюнкции эквивалентна формуле

.

Это позволяет дать определение понятиям нормальных форм исчисления высказываний, которые совпадают с соответствующими определениями алгебры высказываний.

Теорема 3.1. Для каждой формулы 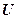исчисления высказываний существуют эквивалентные ей дизъюнктивная и конъюнктивная нормальные формы.