
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод контурных токов
|
|
Расчет методом контурных токов, так как он позволяет сократить число уравнений. При расчёте этим методом полагают, что в каждом независимом контуре схемы течёт свой контурный ток. Уравнения составляют относительно контурных токов, после чего через них определяют токи ветвей.
Если в схеме три контура, то систему уравнений для решения методом контурных токов записывают следующим образом:

В данной системе  ,
, 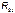 ,
,  - суммы сопротивлений первого, второго и третьего контуров соответственно:
- суммы сопротивлений первого, второго и третьего контуров соответственно:



Сопротивления смежных ветвей  ,
,  ,
,  ,
,  ,
,  ,
,  берут со знаком минус, так как направление контурных токов во всех ветвях встречное (если они по направлению совпадают, то смежное сопротивление берётся со знаком плюс).
берут со знаком минус, так как направление контурных токов во всех ветвях встречное (если они по направлению совпадают, то смежное сопротивление берётся со знаком плюс).



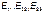 - контурные Э.Д.С. первого, второго и третьего контуров. В них со знаком плюс входят Э.Д.С., направления которых совпадают с направлением обхода контура, минус – Э.Д.С., направленная против направления обхода.
- контурные Э.Д.С. первого, второго и третьего контуров. В них со знаком плюс входят Э.Д.С., направления которых совпадают с направлением обхода контура, минус – Э.Д.С., направленная против направления обхода.



Подставив все получившиеся значения в систему, вычисляем её главный определитель ∆, а также определители ∆ 1, ∆ 2, ∆ 3, полученные при подстановке на место 1-го, 2-го и 3-го столбцов соответственно значений столбца контурных Э.Д.С.
Находим значения контурных токов:
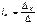

А также токи в ветвях, равные алгебраической сумме контурных токов:
 ,
,  ,
, 
 ,
, 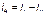 ,
, 
Для того, чтобы проверить правильность расчетов составляют баланс мощностей по формуле:

Если направление тока I, протекающего через Э.Д.С. E, совпадает с направлением Э.Д.С., то произведение EI входит в уравнение с положительным знаком, так как источник Э.Д.С. доставляет в цепь энергию.