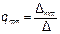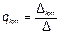Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Принцип наложения и метод наложения
|
|
Ещё один метод расчета линейных электрических цепей называется методом наложения. В его основе лежит принцип наложения, который можно сформулировать следующим образом: ток в любой ветви равен алгебраической сумме токов, вызываемых каждой из Э.Д.С. схемы в отдельности.
 |
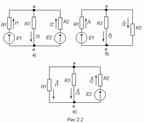
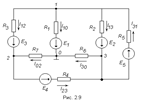
На исходной схеме (рис 2.2а) произвольно выбираем направления токов. Рассчитываем цепь от действия Э.Д.С. Е1, для чего мысленно закорачиваем (убираем) все остальные Э.Д.С., в нашем случае Э.Д.С. Е2 (рис 2.2б).
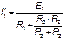
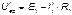
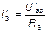
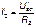
Рассчитываем цепь от действия Э.Д.С. Е2, для чего мысленно закорачиваем Э.Д.С. Е1 (рис 2.2в)
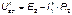
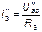
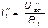
Действительные токи находим как алгебраическую сумму найденных частичных токов. Значения токов 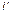 и
и 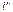 берём со знаком минус, если они направлены в другую сторону, нежели ток на исходной схеме.
берём со знаком минус, если они направлены в другую сторону, нежели ток на исходной схеме.
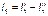
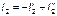
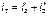
 Входные и взаимные проводимости ветвей
Входные и взаимные проводимости ветвей
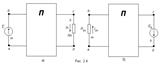
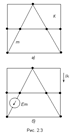 На рис. 2.3а изображена скелетная схема пассивной цепи. В каждой её ветви есть сопротивление. Выделим две схемы ветви m и k. Поместим в ветвь m Э.Д.С. (рис 2.3б). Выберем контуры в схеме так, чтобы k- ветвь входила только в k- контур, а m- ветвь, только в m-контур. Э.Д.С. Em вызовет точки в ветвях m и k.
На рис. 2.3а изображена скелетная схема пассивной цепи. В каждой её ветви есть сопротивление. Выделим две схемы ветви m и k. Поместим в ветвь m Э.Д.С. (рис 2.3б). Выберем контуры в схеме так, чтобы k- ветвь входила только в k- контур, а m- ветвь, только в m-контур. Э.Д.С. Em вызовет точки в ветвях m и k.
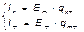
Коэффициенты q имеют размерность проводимости. Коэффициент qmm называют входной проводимостью ветви m, qkm – взаимной проводимостью.
Для расчёта проводимостей составляют уравнения по методу контурных токов, следя за тем, чтобы ветви, взаимные и входные проводимости которых представляют интерес, входили каждая только в свой контур. Далее находят определитель системы ∆ и по нему необходимые алгебраические дополнения.