Новое сечение и расчет.

b=160мм из досок 175мм (ГОСТ 244540890*)

h_y=1221

h_п=495

h_к=396

h_б=1522

После проведения аналогичного расчета получили:

Нагрузка на раму не изменилась.

Опорные реакции:

- вертикальные:

-горизонтальные (распор):

Определяем расчетные усилия.

Усилия в расчетном сечении 1-1 ( м; м) – по оси биссектрисы карнизного узла.

Изгибающий момент

Продольная сила

Где

Тогда

Усилия в сечениях 1-2 и 1-3 карнизного узла:

где м

Точнее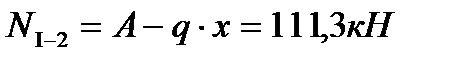

Нормальная сила в коньковом сечении 1-3:

,

где м.

Геометрические характеристики в сечении 1-1 по биссектрисе карнизного узла и в сечении 1-2 и 1-3.

Расчетная площадь

м

Момент сопротивления

Расчетные сопротивления на сжатие умножаются на коэффициент

При высоте сечения больше 50 см коэффициент находим по интерполяции значений табл. 9[5]:

Для высоты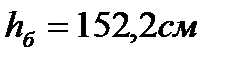

Для высоты

Коэффициент так как толщина слоя клееного сечения рамы принята 33 мм (см. табл.10 [5]), коэффициент по табл. 7[5].

Тогда Мпа

Длина полурамы по осевой линии.

м

;

Для элементов переменного по высоте сечения коэффициент следует умножить на коэффициент , принимаемый по таб.1 СНиП

где

Значение 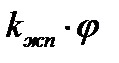не должно быть больше 1, поэтому принимаем

Тогда

где -продольная сила в коньковом сечение 3-3(1-3 на рисунке узла);

кН

где - момент в биссектрисном сечение 1-1

Для перевода напряжении в МПа в соответствии с системой СИ используем коэффициент .

Сжатие вдоль оси «х» под углом к волокнам

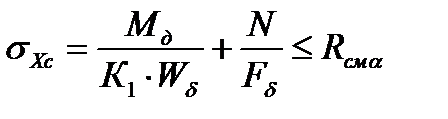
- ВЫПОЛНЯЕТСЯ

где (см. рис. 4)

Растяжение вдоль оси «х» под углом к волокнам

Мпа- НЕ ВЫПОЛНЯЕТСЯ

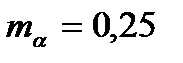; (см. рис. 4)

НЕОБХОДИМО ЕЩЕ УВЕЛИЧИТЬ СЕЧЕНИЕ

b=180мм из досок 200мм (ГОСТ 244540890*)

h _y =1287;

h _п =528;

h _к =396;

h _б =1605.

Распишем геометрические размеры:

Определяем координаты биссектрисного сечения x и y:

м

м

; м- высота между внешней и внутренней точками биссектрисного сечения.

Длина стойки по осевой линии:

м.

Длина ригеля по осевой линии:

,

где м,

где расстояние по высоте между серединами карнизного конькового узлов м, где y¹- расстояние по высоте между внешней точкой карнизного узла и серединой конькового узла м,

где м.

В итоге, м.

Угол наклона осевой линии ригеля к горизонтали:

⁰.

Высота рамы в коньке:

м

Стрела подъема рамы расчетного сечения (по осевой линии):

м

Окончательный расчетный пролет:

≈ 10, 3м.

Из аналогичного расчета получили:

Нагрузка на раму не изменилась.

Опорные реакции:

- вертикальные:

-горизонтальные (распор):

Определяем расчетные усилия.

Усилия в расчетном сечении 1-1 ( м; м) – по оси биссектрисы карнизного узла.

Изгибающий момент

Продольная сила

Где

Тогда

Усилия в сечениях 1-2 и 1-3 карнизного узла:

где м

Точнее

Нормальная сила в коньковом сечении 1-3:

,

Где, м.

Геометрические характеристики в сечении 1-1 по биссектрисе карнизного узла и в сечении 1-2 и 1-3.

Расчетная площадь

м

Момент сопротивления

Расчетные сопротивления на сжатие умножаются на коэффициент

При высоте сечения больше 50 см коэффициент находим по интерполяции значений табл. 9[5]:

Для высоты

Для высоты

Коэффициент так как толщина слоя клееного сечения рамы принята 33 мм (см. табл.10 [5]), коэффициент по табл. 7[5].

Тогда Мпа

Длина полурамы по осевой линии.

м

;

Для элементов переменного по высоте сечения коэффициент следует умножить на коэффициент , принимаемый по таб.1 СНиП

где

Значение 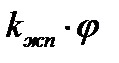не должно быть больше 1, поэтому принимаем

Тогда

где -продольная сила в коньковом сечение 3-3(1-3 на рисунке узла);

кН

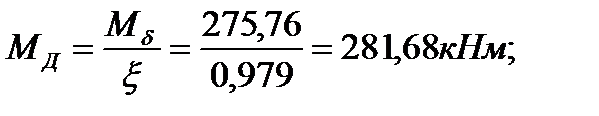
где - момент в биссектрисном сечение 1-1

Для перевода напряжении в МПа в соответствии с системой СИ используем коэффициент .

Сжатие вдоль оси «х» под углом к волокнам

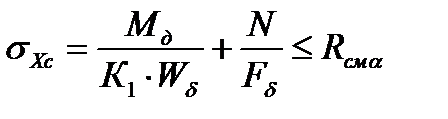
- ВЫПОЛНЯЕТСЯ

где (см. рис. 4)

Растяжение вдоль оси «х» под углом к волокнам

Мпа - ВЫПОЛНЯЕТСЯ

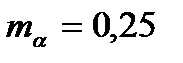; (см. рис. 4)

Сжатие вдоль оси «у» под углом к волокнам

-ВЫПОЛНЯЕТСЯ

(см. рис. 4)

УСЛОВИЯ ПРОЧНОСТИ РАМЫ ОБЕСЕПЕЧЕНЫ!!!

Недонапряжение по одной из проверок прочности должно быть меньше 5%.

Оно составляет:

Окончательно принимаем высоту сечения рамы:

h _y =1287мм; h _п =528мм; h _к =396мм.

Проверка нормальных напряжений в других сечениях стойки рамы не требуется.