Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение закона движения системы.
|
|
Дифференциальное уравнение движения механической системы:
+ 2п 
+ k2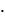 
S = h0 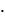sin(pt),
Где 
Проинтегрируем дифференциальное уравнение. Общее решение этого неоднородного дифференциального уравнения складывается из общего решения однородного уравнения SOD ичастного решения неоднородного Sч: S = SOD+ Sч. Однородное дифференциальное уравнение, соответствующее данному неоднородному, имеет вид:
+2n 
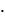+k2 S=0.
Решение этого уравнения ищем в виде функции:
где А и 
- неопределенные постоянные величины.
Подставляя эту функцию в предыдущее уравнение, получим:
Так как мы ищем нетривиальное решение, то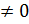 
. Следовательно, должно выполняться условие:
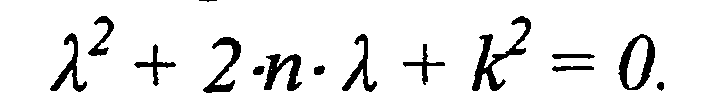
Находим корни этого характеристического уравнения:
Так как п < k решение однородного уравнения имеет вид:
Где 
Частное решение дифференциального уравнения ищем в виде правой части:
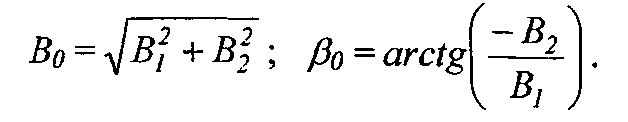Где
Подставляя в выражение, после несложных преобразований получаем:
Сравнивая коэффициенты при соответствующих тригонометрических функциях справа и слева получаем систему алгебраических уравнений для определения постоянных В1 и В2:
Решая эту систему, получаем следующие выражения:
Таким образом, получаем общее решение дифференциального уравнения в виде:
Постоянные интегрирования А0 и α 0 определяются из начальных условий, при t = 0 имеем:
Решая эту систему, получаем:
рад
Закон движения системы имеет вид:
