
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Умножением множеств.
|
|
Декартово умножение не обладает переместительным свойством, т. е. существуют такие
множества А и В, что А ХВ 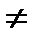 ВХА. Чтобы убедиться в этом, достаточно образовать
ВХА. Чтобы убедиться в этом, достаточно образовать
декартовы произведения АХВ и ВХА для таких, например, множеств: А={1, 2, 3}, В = {3,
5}. Множество АХВ получено нами раньше, а множество ВХА таково: {(3, 1), (3, 2), (3, 3),
(5, 1), (5, 2), (5, 3)}. Нетрудно видеть, что АХВ 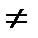 ВХА, так как множества АХ.В и ВХА
ВХА, так как множества АХ.В и ВХА
состоят из различных элементов.
Декартово умножение множеств не подчиняется и сочетательному закону, но связано с
операцией объединения множеств распределительным свойством: для любых множеств А,
ВиС имеет место равенство (A 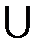 B)ХС = (АХС)
B)ХС = (АХС) 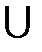 (BXC).
(BXC).
Его мы примем без доказательства.
Элементы декартова произведения двух конечных множеств удобно записывать при
помощи прямоугольной таблицы. Например, декартово произведение множеств
А = {1, 2, 3} иВ= {3, 5} можно представить в следующем виде: