
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнения прямой в пространстве
|
|
Прямая в пространстве
Уравнения прямой в пространстве
Напомним, что в аналитической геометрии любая пространственная линия рассматривается как пересечение двух поверхностей.
Так как каждая прямая всегда может быть помещена в некоторую плоскость и при пересечении двух плоскостей образуется прямая, то в аналитической геометрии прямую в пространстве принято задавать как пересечение двух плоскостей.
Итак, пусть  и
и  – уравнения любых двух различных плоскостей, содержащих прямую
– уравнения любых двух различных плоскостей, содержащих прямую  . Тогда координаты любой точки прямой
. Тогда координаты любой точки прямой  удовлетворяют одновременно обоим уравнениям, т.е. являются решениями системы
удовлетворяют одновременно обоим уравнениям, т.е. являются решениями системы
 (1)
(1)
Систему (1) называют общими уравнениями прямой в пространстве. Так как через любую прямую в пространстве проходит множество плоскостей, то любую прямую можно задать ее общими уравнениями и не единственным образом.
Недостатком задания прямой общими уравнениями является то, что по их виду ничего нельзя сказать о расположении прямой в пространстве. При решении задач удобнее использовать другие, более наглядные формы записи уравнений прямой – параметрические или канонические уравнения.
Получим параметрические и канонические уравнения прямой в пространстве, решив следующую задачу.
ЗАДАЧА 1. Записать уравнение прямой в пространстве, проходящей через точку  , параллельно вектору
, параллельно вектору  .
.
Также, как и для прямой на плоскости, вектор, параллельный прямой в пространстве, называют направляющим вектором этой прямой.
 Пусть
Пусть  – текущая точка прямой. Обозначим через
– текущая точка прямой. Обозначим через  и
и  – радиус-векторы точек
– радиус-векторы точек  и
и  .
.
Рассмотрим векторы 
 и
и  . По условию задачи они параллельны.
. По условию задачи они параллельны.
Следовательно, существует такое число  (
( называют параметром), что
называют параметром), что

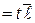 ,
,

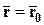
 , (2*)
, (2*)
или, в координатной форме,
 (2)
(2)
Уравнение (2*) и систему уравнений (2) называют параметрическими уравнениями прямой в пространстве (в векторной и координатной форме соответственно).
Если в задаче 1 вектор  не параллелен ни одной из координатных плоскостей (т.е. если
не параллелен ни одной из координатных плоскостей (т.е. если  ,
,  и
и 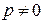 ), то из уравнений системы (2) можно выразить параметр
), то из уравнений системы (2) можно выразить параметр  :
:
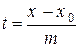 ,
,  ,
, 
и заменить систему (2) одним равенством вида:


 . (3)
. (3)
где  – координаты некоторой точки на прямой;
– координаты некоторой точки на прямой;  ,
, 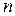 ,
,  – координаты направляющего вектора прямой.
– координаты направляющего вектора прямой.
Уравнения (3) называют каноническими уравнениями прямой в пространстве.
 Частным случаем канонических уравнений являются уравнения прямой, проходящей через две заданные точки.
Частным случаем канонических уравнений являются уравнения прямой, проходящей через две заданные точки.
Действительно, пусть прямая проходит через две точки  и
и  . Тогда вектор
. Тогда вектор


является ее направляющим вектором, и канонические уравнения этой прямой будут иметь вид
 . (4)
. (4)
Уравнения (4) называют уравнениями прямой, проходящей через две заданные точки  и
и  .
.