
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Взаимное расположение прямых в пространстве
|
|
Если в пространстве даны две прямые, то они могут 1) быть параллельны, 2) пересекаться, 3) скрещиваться.
Выясним, как по уравнениям прямых определить их взаимное расположение.
Пусть прямые  и
и  заданы каноническими уравнениями:
заданы каноническими уравнениями:
 :
: 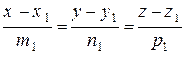 ,
,  :
:  .
.
 Если прямые параллельны, то их направляющие векторы
Если прямые параллельны, то их направляющие векторы
 и
и 
коллинеарные. Так как коллинеарные векторы имеют пропорциональные координаты, то условие параллельности прямых будет иметь вид:
 . (7)
. (7)
 Теперь рассмотрим две пересекающиеся прямые. Такие прямые можно поместить в одну плоскость. Но это значит, что векторы
Теперь рассмотрим две пересекающиеся прямые. Такие прямые можно поместить в одну плоскость. Но это значит, что векторы  ,
,  и
и 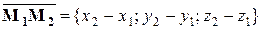 будут компланарны. Следовательно,
будут компланарны. Следовательно,
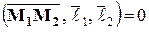 , (8)
, (8)
или, в координатной форме,
 . (9)
. (9)
Таким образом, если прямые  и
и  не параллельны и для них выполняется условие (8) (или, в координатной форме, условие (9)), то они пересекаются.
не параллельны и для них выполняется условие (8) (или, в координатной форме, условие (9)), то они пересекаются.
Так как скрещивающиеся прямые нельзя поместить в одну плоскость, то для скрещивающихся прямых условие (8) не выполняется. Следовательно, если прямые  и
и  не параллельны и для них не выполняется условие (8) (или, в координатной форме, условие (9)), то они скрещиваются.
не параллельны и для них не выполняется условие (8) (или, в координатной форме, условие (9)), то они скрещиваются.
НАПРИМЕР. Прямые
 :
:  и
и  :
: 
будут параллельны, так как их направляющие векторы  и
и  удовлетворяют условию (7):
удовлетворяют условию (7):
 .
.
Прямые
 :
:  и
и  :
: 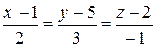
не являются параллельными (их направляющие векторы не коллинеарны) и для них выполняется условие (9):
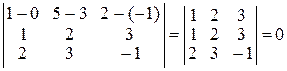
Следовательно, прямые  и
и  – пересекаются.
– пересекаются.
И, наконец, рассмотрим прямые
 :
:  и
и  :
: 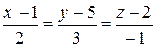 .
.
Они не являются параллельными (их направляющие векторы не коллинеарны) и для них не выполняется условие (9):
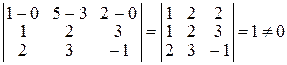
Следовательно, прямые  и
и  – скрещиваются.
– скрещиваются.