ЛЕКЦІЯ №1.

ТЕМА: «Визначники, їх властивості, розв’язання систем лінійних рівнянь за формулами Крамера.»

ПЛАН:

1. Означення визначника та визначення усіх його складових.

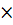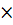2. Правила обчислення визначників 2 2, 3 3.

3. Основні властивості визначників.

4. Правила обчислення визначників любого порядку.

5. Розв'язання систем лінійних рівнянь за формулами Крамера.

ХІД ЛЕКЦІЇ:

1. Визначником - го порядку або детермінантом (від лат. determino − визначаю) називається число 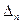, яке відповідає квадратній таблиці:

(1.1)

де 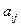називаються елементами визначника (всього їх ). Індекс 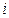вказує на номер рядка, а - номер стовпця квадратної таблиці (1.1).

Головною діагоналлю визначника називається сукупність елементів

Мінором 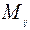елемента 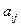квадратної матриці (1.1) називають визначник -го порядку 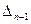, отриманий з визначника 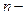го порядку 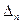викреслюванням 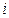-го рядка та -го стовпця.

Алгебраїчне доповнення елемента 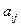визначається рівністю .

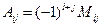2. Для

. (1.2)

Узагальнимо правило обчислення визначника на більшу кількість елементів, тобто на визначники матриць більшого порядку. Нехай . Для обчислення таких визначників можна скористатись методом діагоналей.

Правило трикутника або зірки:

Метод діагоналей (правило Саррюса): визначник матриці дорівнює сумі добутків елементів головних діагоналей мінус сума добутків елементів побічних діагоналей. Наприклад, правило Саррюса обчислення визначника 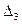(буде рівносильним відомому правилу трикутника) має вигляд:

- - - + + +

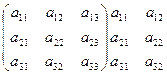
У відповідності з цією схемою маємо:

(1.4)