Розв'язання систем лінійних рівнянь за формулами Крамера.

Системою m лінійних рівнянь з n змінними x₁, x₂, …, x_n називається система, яка має наступний вигляд:

де а_ij – коефіцієнти при змінних; b_i -вільні члени,

Упорядкована сукупність чисел , називається розв’язком системи, якщо при заміні х₁ на а₁, х₂ на а₂, …, х_n на а_n у кожному рівнянні системи дістанемо n правильних числових рівностей.

Система, що має розв’язок, називається сумісною. Система, яка не має жодного розв’язку, називається несумісною. Система з єдиним розв’язком називається визначеною, а з більшим числом розв’язків – невизначаною.

Розглянемо формули Крамера для системи лінійних рівнянь з трьома невідомими:

(1.6)

Формули Крамера для системи (1.6) мають вигляд:

,

де 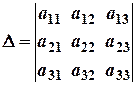- визначник системи (1.6), а

визначники, які дістають з визначника заміною першого, другого і третього стовпців відповідно стовпцем вільних членів.

Система (1.6) має:

а) єдиний розв’язок, коли ;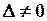

б) безліч розв’язків, коли

в) не мати жодного розв’язку, коли і хоча б один із визначників відмінний від нуля.

ЛІТЕРАТУРА:

1. Пастушенко С.М. Вища математика: Довідник для студентів вищих навч.закладів: Навч.посібник / Пастушенко С.М., Ю.П.Підченко. –К.: Діал, 2006.–464с.

2. Литвин І.І. Вища математика. Навчальний посібник / Литвин І.І., Конончук О.М., Желізняк Г.О.– Київ: Центр навчальної літератури, –2004.–368с.