Основні властивості визначників.

1. Значення визначника не змінюється, якщо його рядки замінити відповідними стовпцями, а стовпці – рядками.

2. Перестановка двох рядків (стовпців) визначника рівносильна множенню його на –1.

3. Якщо визначник має два однакових рядка (стовпця), то він дорівнює нулю.

4. Якщо всі елементи якого-небудь рядка (стовпця) визначника містять спільний множник, то його можна винести за знак визначника.

5. Якщо всі елементи деякого рядка (стовпця) визначника дорівнюють нулю, то і сам визначник дорівнює нулю.

6. Якщо відповідні елементи двох рядків (стовпців) визначника пропорційні, то визначник дорівнює нулю.

7. Якщо кожний елемент деякого рядка (стовпця) визначника є сумою двох доданків, то визначник дорівнює сумі двох визначників, у яких один у згаданому рядку (стовпці) має перші з заданих доданків, а інший – другі; елементи, що знаходяться на решті місць, у всіх трьох визначниках одні й ті самі. Записується ця властивість таким чином:

.

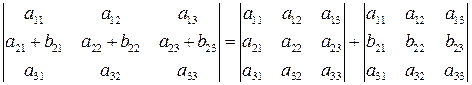8. Якщо до елементів деякого рядка (стовпця) визначника додати відповідні елементи іншого рядка (стовпця), помножені на довільний спільний множник, то значення визначника при цьому не зміниться.

4. Правила обчислення визначників любого порядку:

- Метод розкладання: Визначник дорівнює сумі добутків елементів рядка (стовпця) на їхні алгебраїчні доповнення. Наприклад, для першого рядка маємо:

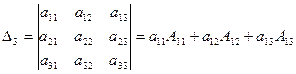, (1.5)

де

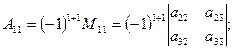
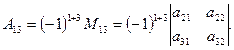
Величини - алгебраїчні доповнення, а 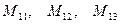- мінори визначника 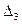, що відповідають його елементам . Ці мінори є визначниками другого порядку і отримані із визначника 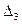викресленням відповідних рядка і стовпця.

Зауваження 1. Метод розкладання дає можливість обчислювати визначники довільного порядку. Так, наприклад, визначник четвертого порядку зводиться до обчислення чотирьох визначників третього порядку, визначник п’ятого порядку – до обчислення п’яти визначників четвертого порядку, тобто – двадцяти визначників третього порядку і т. д. Такий спосіб обчислення визначників вищих порядків громіздкий, тому іноді доцільніше користуватися іншими методами обчислення визначників.

- Метод ефективного зниження порядку. Використовуючи основні властивості визначників, обчислення завжди можна звести до обчислення одного визначника 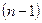-го порядку, зробивши в будь-якому рядку 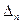всі елементи, крім одного, рівними нулю.

- Зведення визначника до трикутного вигляду. Визначник, у якого всі елементи, що знаходяться вище або нижче головної діагоналі, рівні нулю, називається визначником трикутного виду. Очевидно, що в цьому випадку визначник дорівнює добутку елементів його головної діагоналі. Зведення будь-якого визначника 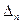до трикутного виду завжди можливе.