Решение задачи двух тел

Согласно третьему закону Ньютона силы, с которыми тела действуют друг на друга, равны по величине и противоположны по направлению. Таким образом, для задачи двух тел можно записать

Проинтегрировав это уравнение два раза, получим

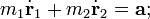
где a и b – некоторые векторы.

Обозначив через R и M координату центра тяжести двух тел и их суммарную массу соответственно

получим

то есть центр масс системы движется с постоянной скоростью.

Запишем силы, действующие на каждое из тел, следующим образом

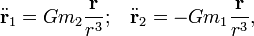где

Вычитая второе уравнение из первого, получим

где

Векторно умножая последнее уравнение на r и интегрируя, получим

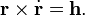
Постоянный вектор h, являющийся постоянной интегрирования, называется кинетическим моментом системы. Взаимное движение тел происходит в плоскости, перпендикулярной этому вектору. Введём систему цилиндрических координат r, φ, z. Единичные векторы вдоль радиальной, трансверсальной и вертикальной оси обозначим как i, j и k. Проекции скорости на радиальную и трансверсальную оси составят

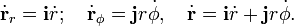
Тогда

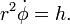
В левой части последнего выражения стоит удвоенная площадь треугольника, описываемого радиус-вектором r за единицу времени. Таким образом, это соотношение является математической записью второго закона Кеплера.

Уравнение (1) умножаем скалярно на скорость и интегрируем. Получим

Подробный вывод

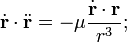
Распишем последнее выражение в координатах:

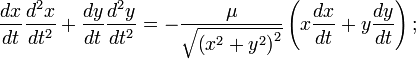
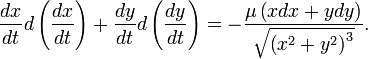
Заметим, что

Тогда

Интегрируя обе части, получим

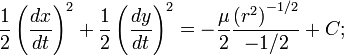
Последнее соотношение является выражением закона сохранения механической энергии в системе.