
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теплофизические (тепловые) свойства мерзлых грунтов. Знание теплофизических свойств мерзлых грунтов необходимо для расчета температуры – показателя их теплового состояния
|
|
Знание теплофизических свойств мерзлых грунтов необходимо для расчета температуры – показателя их теплового состояния. Коротко остановимся на основных закономерностях температурного режима литосферы.
Температура литосферы, в том числе и в области распространения вечномерзлых грунтов (криолитосферы) определяется климатическими (граничными, внешними) условиями и ее теплофизическими свойствами: коэффициентом теплопроводности l, ккал / м.час.град (или Вт / м.град; Вт = 1, 16 ккал / час); объемной теплоемкостью Соб, ккал / м3 и коэффициентом температуропроводности а, м2 / час. Эти три характеристики зависят отсостава и физических свойств грунта и связаны между собой соотношением а= l /С об.
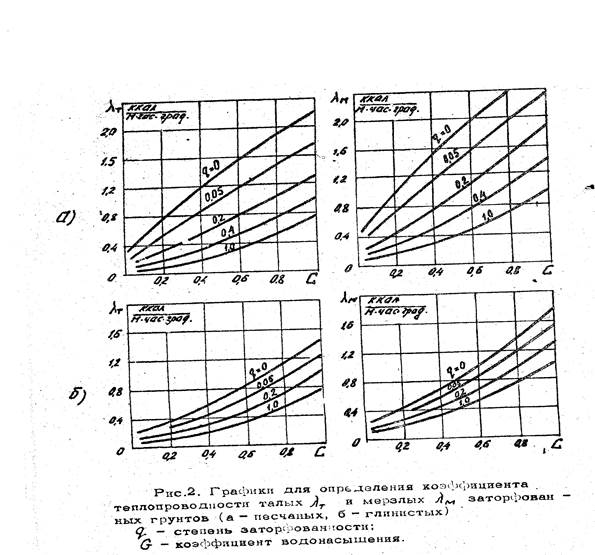
Коэффициент теплопроводности представляет собой коэффициент пропорциональности между потоком тепла q и градиентом температуры g в выражении теплового потока q = l.g. Он характеризует способность материала проводить тепло, зависит от вида материала и его физических свойств, главным образом от плотности и влажности. Установлено, что обобщенным эквивалентом этих двух характеристик, по крайней мере, у грунтов является степень влажности G (А.А. Коновалов, Л.Т. Роман, СНиП II-18-76). На рис.4 (2) показана зависимость l от G у мерзлых и талых грунтов по данным этих авторов. Из него видно, что величина l (ккал / м.час.град) повышается в ряду: торф – глина – суглинок – супесь – песок; в талом состоянии, примерно от 0, 1…0, 8 у торфов до 0, 4…2, 4 у песков; в мерзлом – на 20 -30% больше. Это объясняется тем, что l льда примерно в 4 раза выше l воды (1, 9 и 0, 48 ккал / м.час.град).
Теплоекость определяется количеством тепла, которое надо сообщить выделенному объему грунта для повышения его температуры и характеризует тепловую инерцию. Различают удельную теплоемкость Су, равную количеству тепла необходимого для нагрева 1 грамма грунта на 1оС, и объемную Соб= Су. r, которая рассчитывается на единицу объема грунта.
Удельная теплоемкость для каждого вида грунта примерно постоянная величина. У песков она составляет 0, 17 ккал / к г .град; у супесей, суглинков и илов – 0.18…0, 20; у глин – 0, 22; у торфов – 0, 38. У воды и льда она равна 0, 5 и 1 ккал / к г .град, соответственно. Теплоемкость, так же как масса и объем (в отличие от тепло- и температуропроводности) подчиняется правилу аддитивности (суммирования) и может рассчитываться как средневзвешенная величина по соотношению теплоемкостей и компонентов грунта
К теплофизическим показателям относятся также коэффициент теплоотдачи a, ккал / м2.час.град (Вт / м2.град), и скрытая теплота плавления (кристаллизации) Qпл - практически постоянная величина (несколько уменьшающаяся при понижении температуры), равная 80000 ккал / м3 (334000 кДж / м3=334 МПа) или в пересчете на объемную массу Qпл / r = 80 ккал /кг = 334 кДж /кг. Теплофизическим параметром по своему физическому смыслу является и уже рассмотренная выше температура замерзания (оттаивания) и конечно собственно температура грунта t, oC.
И так – всего 7 теплофизических параметров ( l, С, а, a, Qпл, t к, t).
Экспериментальное определение теплофизических характеристик.
Коэффициент температуропроводности и теплоемкость грунтов определяется на калориметрических установках (подобных применяемым для определения количества незамерзшей воды) методом регулярного режима.
При охлаждении или нагревании тела в среде с постоянной температурой tс происходит выравнивание температурного профиля. Если тело лишено внутренних источников тепла, то в процессе теплообмена можно выделить стадию упорядоченного охлаждения или нагревания, называемую регулярным режимом. Она характеризуется тем, что распределение разности температур |t—tс|=h в различных точках тела изменяется во времени по одному закону (экспоненциальному) и определяется формой, размером, теплофизическими характеристиками тела и условиями теплообмена на границе тела со средой.
При этом темп охлаждения (нагревания) может быть найден опытным путем как тангенс угла наклона прямой на графике lnh=f(t), построенном для любой точки тела. Связь темпа охлаждения (m) с температуропроводностью (а) определяется формулой: m = а/Ь, где b — фактор формы, который рассчитан теоретически для тел правильной формы: шара, цилиндра и параллелепипеда. В частности для цилиндрических образцов, фактор формы рассчитывается по формуле
b =1/[(2, 4048/r) 2+ (3, 14/H) 2], (**)
где r и H — радиус и высота образца.
Конструкция лабораторной установки представлена на рисунке.

Схема прибора для определения температуропроводности методом регулярного режима I рода:
1 — образец грунта; 2 — дифференциальная термопара; 3 — термостатирующая жидкость; 4 — сетка для образца; 5— мешалка; 6 —термометр; 7 - термостатирующая оболочка, заполненная эвтектической смесью; 8 - измерительный прибор
Образец грунта диаметром 3—4 и высотой 4—6 см помещается в латунный стаканчик), в крышке которого закреплена медно-константановая термопара 2 так, чтобы один спай ее находился в центре образца, а второй— в окружающей среде. Термопара подключается к измерительному прибору (гальванометру или милливольтметру), который позволяет измерить разность температур между средой и образцом с точностью ±0, 1° С. Для автоматической записи температуры можно использовать самопишущий потенциометр подходящей чувствительности. Согласно теории метода в среде, куда погружается исследуемый образец грунта, поддерживается постоянная температура и обеспечивается достаточно большой теплообмен образца со средой. Термостат, удовлетворяющий этим условиям, состоит из двух частей: термостатирующей оболочки 7, заполненной эвтектической смесью, и внутреннего бачкас термостатирующей жидкостью 3, в котором находится мешалка 5, обеспечивающая энергичное перемешивание жидкости.
Подготовка образца. Испытания можно проводить с грунтами естественного и нарушенного сложения при положительных и отрицательных температурах. Определяют высоту, диаметр и массу пустого калориметра. Образцы естественного сложения вырезают из монолита непосредственно в стаканчик калориметра так, чтобы между стенками и грунтом не было воздушных зазоров. Влажность грунта определяют до и после опыта. Для образцов нарушенного сложения готовится грунт заданной влажности, который уплотняется в калориметре до заданного значения объемного веса. Заполненный калоримётр взвешивают и закрывают крышкой с термопарой, зазоры между крышкой, стаканчиком и дном герметизируют.
Проведение опыта. Если опыт проводится при положительных температурах, то образцы выдерживают при комнатной температуре около 30 мин. Оболочку термостата наполняют смесью воды со льдом, а внутренний бачок — водой температурой 0° С.
При отрицательных температурах образцы выдерживают в холодильном шкафу при температуре —10° С в течение нескольких часов для установления теплового равновесия. Защитная оболочка термостата заполняется эвтектической смесью с температурой плавления около —20° С (обычно 22, 4%-ный раствор МаС1), а рабочий объем — спиртом при той же температуре. Опыт может проводиться и в цикле повышения температуры, когда, как правило, образцы выдерживаются при —20° С, а термостат — при —10° С (19, 7%-ный раствор КС1).

|
| Рис.. Пример расчета опыта по определению температуропроводности |
Включается мотор мешалки и через 15 — 20 мин начинается опыт. Термопара подключается к измерительному прибору, калориметр вместе с контрольным спаем термопары погружается в
жидкость термостата, включается секундомер и регистрируются изменения температуры и время т.
По полученным данным строится график lnh=f(t) (cм. рис.), на нем выбирается прямоугольный участок, для которого рассчитывается величина m
m=(lnh1–lnh2)/(t2–t1)=(3, 8–2, 48)/(126–33)=0, 0142с-1
Размеры образца в примере на рис.: Н=6, 03см, 2r=3, 8см, тогда фактор формыкалориметра, рассчитанный по формуле (**), равен b=0, 54.10-4 м2
Теперь определяем коэффициент температуропроводности
а=bm=0, 767.10-6 м2/с =0, 0028 м2/час.