Вивчення нового матеріалу.

ХІД УРОКУ

Організація учнів.

Повторення раніше вивченого матеріалу.

Усне опитування.

(питання до учнів типу де можна на практиці застосувати ці знання, в якій професії вони використовуються та інші).

Вивчення нового матеріалу.

1. Поділ кола на рівні частини частини.

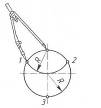В побудовах зображень часто виникає необхідність поділу кола на рівні частини. Найчастіше треба поділити коло на 3 і на шість частин. Поділ краще та швидше виконувати за допомогою циркуля.

Поділ кола на три частини дуже простий. Креслимо коло необхідного діаметра. Залишаємо відстань між олівцем та голкою циркуля незмінною. Ставимо голку циркуля на одну з точок перетину кола та центрової лінії. Проводимо дугу. Перетин дуги з колом утворюють дві точки. Третя точка розміщена на протилежному боці кола в точці перетину центрової лінії та кола.

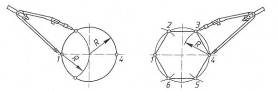
Поділ кола на 6 частин дуже схожий. Перший крок – поділ кола на три частини. Наступний – ставимо голку в протилежну точку перетину центрової лінії та кола і проводимо дугу. Перетин дуги з колом утворюють ще дві точки. Ще дві точки – це точки, в які ставилась голка.

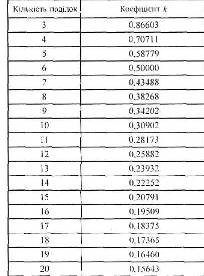
Поділ на 5, 7, та більше частин за допомогою циркуля складна справа. Тому краще використовувати таблицю хорд. В ній подані коефіцієнти k, які необхідно помножити на діаметр кола d: l=d·k. Знаючи довжину хорди ми вставляємо циркуль або вимірник на цю величину і з однієї точки відкладаємо по колу засічки. Якщо перша і остання засічки співпадуть то поділ виконаний точно.

Плавний перехід однієї лінії контура зображення в ін­шу називають спряженням. Всі спряження на кресленні виконують дугамрі кіл заданих радіусів. Точку, з якої проводять дугу плавного переходу однієї лінії до іншої, називають центром спряження.

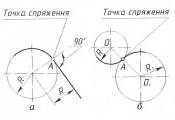Перехід від одного кола до іншого буде плавним тоді, коли ці кола дотикаються. Точка спряження двох кіл ле­жить на прямій, що сполучає центри спряжуваних кіл. Отже, побудова спряження завжди зводиться до визна­чення центра і точок спряження. Побудувавши центр спря­ження циркулем, розхил якого дорівнює радіусу спряжен­ня, між точками спряження проводять дугу. Вона і буде утворювати плавний перехід від однієї лінії контура зобра­ження до іншої.

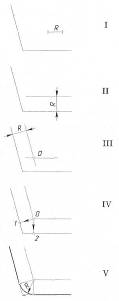
Дві прямі, що перетинаються, можуть утворювати прямий, гострий і ту­пий кути. Для всіх трьох випадків спосіб побудови один і той же. Він полягає ось у чому. Дуга плавного переходу від одні­єї прямої до іншої має радіус R. Якщо це дуга кола, то для її проведення слід знати положення центра цього кола.

Послідовність побудови спряження двох прямих, що перетинаються (І).

1. Паралельно першій із спряжуваних прямих проводять допоміжну пряму на відстані радіуса спряження R від неї (ІІ).

2. Паралельно другій із спряжуваних прямих проводять
другу допоміжну пряму, також на відстані радіуса спряження Rвід неї (III). У точці перетину обох допоміжних прямих міститься центр спряження О.

3. З точки Опроводять перпендикуляри на спряжувані
прямі. Утворені точки є точками спряження (IV).

4. Поставивши опорну ніжку циркуля в точку О, розхи­лом циркуля, що дорівнює радіусу спряження R, між точка­ми спряження проводять дугу, яка утворює плавний перехід від однієї прямої до іншої (V).

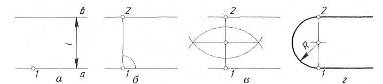
Спряження двох паралельних прямих. Через точки спряження 1 і 2 проводимо перпендикуляр h. Ділимо його пополам. В центрі перпендикуляра ставимо циркуль, відстань між голкою і олівцем рівна h/2.

Спряження дуги кола з прямою відбувається майже аналогічно спряженню двох прямих, що перетинаються. Відмінним є проведення допоміжної біля дуги. Ми проводимо її циркулем радіусом рівним сумі радіусу дуги та радіуса спряження.