
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
III. Полное исследование функции.
|
|
Приведенные выше теоретические сведения по определению интервалов монотонность функции, ее экстремумов, интервалов выпуклости и вогнутости графика функции, его точек перегиба и асимптот позволяют провести полное исследование функции и построить ее график, дающий представление о характерных свойствах и особенностях исследуемой функции. Полное исследование функции проводится по следующему примерному плану:
1. Находится область допустимых значений (ОДЗ) функции.
2. Выясняется, является ли функция четной, нечетной, периодической или общего вида.
3. Определяются точки пересечения с осями координат графика функции, находятся ее нули и точки разрыва.
4. Находятся интервалы знакопостоянства функции.
5. Находятся критические точки, интервалы возрастания, убывания и точки экстремума, а так же характер экстремума в каждой точке.
6. Находятся вертикальные и наклонные асимптоты графика функции.
7. Определяются интервалы выпуклости, вогнутости и точки перегиба графика функции.
8. Для большей точности графика иногда строятся и отдельные точки графика.
9. Строится график функции.
Ниже приводятся примеры полного исследования и построения графиков различных видов функций. По ходу исследования приводятся при необходимости соответствующие пояснения.
Пример 1. Исследовать функцию  и построить ее график.
и построить ее график.
Решение. 1. Функция  определена всюду, кроме точек
определена всюду, кроме точек
 и
и  , поэтому ее ОДЗ включает интервалы
, поэтому ее ОДЗ включает интервалы 
2. Функция  нечетная, так как
нечетная, так как  , следовательно, график функции симметричен относительно начала координат. Функция не периодическая.
, следовательно, график функции симметричен относительно начала координат. Функция не периодическая.
3. Точки пересечения графика функции с осями координат: с осью  при
при  ; с осью
; с осью 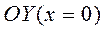 при
при  , т.е. кривая
, т.е. кривая  проходит через начало координат.
проходит через начало координат.
4. Для определения интервалов знакопостоянства построим кривую знаков (рис.6)
 |
Рис.6
Из рис. 6 следует, что данная функция:
положительна в интервалах  и
и
отрицательна в интервалах 
5. Для нахождения критических точек вычислим производную  :
:
 Производная равна нулю в точках
Производная равна нулю в точках  и
и  и не существует в точках
и не существует в точках  ,
,  . Так как точки
. Так как точки  и
и  не входят в ОДЗ функции, то критическими точками не являются. " Подозрительными" на экстремум являются точки
не входят в ОДЗ функции, то критическими точками не являются. " Подозрительными" на экстремум являются точки  и
и  . С помощью первого достаточного признака экстремума (теорема 3.) определим существование и характер экстремумов в этих точках, вычисляя знак
. С помощью первого достаточного признака экстремума (теорема 3.) определим существование и характер экстремумов в этих точках, вычисляя знак  в малой окрестности точек
в малой окрестности точек  и
и 
а) для 

В силу теоремы 3, в точке  функция имеет максимум.
функция имеет максимум.
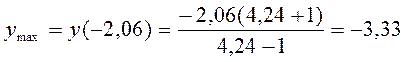
б) Для 

так как производная меняет знак с " - " на " +" при переходе через точку  , то в этой точке функция имеет минимум:
, то в этой точке функция имеет минимум:

Кривая знаков производной имеет вид (см. рис. 7):
 |
Рис.7.
Из рис. Следует, что функция возрастает  на интервалах
на интервалах  и убывает
и убывает  на интервалах
на интервалах 
6. Асимптоты.
а) Очевидно, что при  и
и  , поэтому
, поэтому  и
и 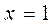 вертикальные асимптоты.
вертикальные асимптоты.
б)  ,
, 

 .
.  - наклонная асимптота.
- наклонная асимптота.
7. Для нахождения интервалов выпуклости вогнутости вычислим  и рассмотрим кривую знаков
и рассмотрим кривую знаков  (см. рис. 8)
(см. рис. 8)

 |
рис. 8.
Вторая производная равна нулю при  и не существует при
и не существует при 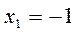 и
и  (точки не входят в ОДЗ).
(точки не входят в ОДЗ).

 Так как при
Так как при  кривая выпукла, а при
кривая выпукла, а при  - выгнута, то график функции выпуклый на интервалах
- выгнута, то график функции выпуклый на интервалах  и выгнутый на интервалах
и выгнутый на интервалах  , что отмечено знаками
, что отмечено знаками  и
и  в таблице, которую удобно использовать при построении графика, в этой таблице знаками и отмечено возрастание, и убывание функции
в таблице, которую удобно использовать при построении графика, в этой таблице знаками и отмечено возрастание, и убывание функции

| 
| 
| 
| 
| 
| 
|

| - | - | + | - | + | + |
 
| ||||||

| 
| 
| 
| 
| 
| 
|