
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Из таблицы следует, что меняет знак при переходе через точку , но тогда по теореме 6 эта точка является абсциссой точки перегиба.
|
|
8. Учитывая результаты исследования, строим график заданной функции (рис. 9.)

Рис. 9.
Первая производная равна нулю при 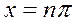 и не существует в точках
и не существует в точках  , которые вне ОДЗ, и критическими не являются. Для нахождения характера экстремума используем второй достаточный признак (см. теорему 4.)
, которые вне ОДЗ, и критическими не являются. Для нахождения характера экстремума используем второй достаточный признак (см. теорему 4.)

В критической точке 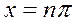 .
.
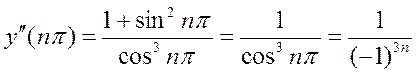 ;
;
отсюда следует, что при четном 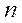
 и в таких точках функция имеет минимум; при нечетном
и в таких точках функция имеет минимум; при нечетном 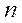
 , и в таких точках функция имеет максимум.
, и в таких точках функция имеет максимум.
На рассматриваемом отрезке в точках  и
и 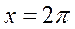 функция имеет минимум.
функция имеет минимум.
 , а в точке
, а в точке 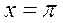 - максимум.
- максимум.
 .
.
Интервалы возрастания и убывания функции найдем по закону  , который определяется знаком
, который определяется знаком  (числителя):
(числителя):
 на интервалах
на интервалах  , следовательно, на этих интервалах функция возрастает;
, следовательно, на этих интервалах функция возрастает;
 на интервалах
на интервалах  , следовательно, на этих интервалах функция убывает.
, следовательно, на этих интервалах функция убывает.
6. а) Вертикальные асимптоты проходят через точки разрыва второго рода, их уравнения
 ,
,
на рассматриваемом отрезке  и
и  .
.
б) Наклонных асимптот функция не имеет, так как второй из пределов (11) не существует.
7. Вторая производная  , знак которой определяется знаком
, знак которой определяется знаком  (знаменателя), на рассматриваемом промежутке положительна при
(знаменателя), на рассматриваемом промежутке положительна при 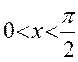 и
и  и отрицательна при
и отрицательна при  . Следовательно, кривая
. Следовательно, кривая  вогнута на интервалах
вогнута на интервалах  и
и  , и выпукла на интервале
, и выпукла на интервале  .
.
Вторая производная  меняет знак при переходе через точки
меняет знак при переходе через точки  , которые в ОДЗ заданной функции не входят и поэтому абсциссами точек перегиба не являются, т. е. функция
, которые в ОДЗ заданной функции не входят и поэтому абсциссами точек перегиба не являются, т. е. функция  точек перегиба не имеет.
точек перегиба не имеет.
8. На основе выводов по каждому пункту составляем для удобства построения графика таблицу. Строим график (рис. 11) для отрезка  и продлеваем его на всю ось
и продлеваем его на всю ось  , используя периодичность заданной функции.
, используя периодичность заданной функции.

| 
| 
| 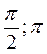
| 
| 
| 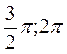
| 
|

| + | - | -1 | - | + | ||
 
| |||||||

| -1 |

Рис.11
Пример 4. Исследовать функцию  и построить ее график.
и построить ее график.
Решение. 1.ОДЗ находим из неравенства 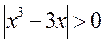
Так как по определению модуля:

 ,
,
то, очевидно, ОДЗ данной функции является вся числовая ось  за исключением точек, где
за исключением точек, где  , т.е. точек:
, т.е. точек:  и
и  .
.
Эти точки разбивают числовую ось на интервалы, в которых данная функция может быть выражена (принимая во внимание определение модуля) следующими аналитическими уравнениями:
а)  если
если  и
и 
б)  если
если  и
и 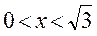
Отметим это на рисунке 12.
 |
Рис. 12.
2. Данная функция - четная, ее график симметричен относительно оси  . Поэтому исследуем функцию для
. Поэтому исследуем функцию для  , а при построении графика воспользуемся симметрией и продлим его для
, а при построении графика воспользуемся симметрией и продлим его для 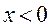 .
.
3. При  рассмотрим функцию
рассмотрим функцию  и
и  :
:
 где
где 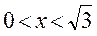 и
и
 где
где  .
.
Обе эти функции общего вида с осью  не пересекаются, а с осью
не пересекаются, а с осью 
 пересекаются в точках, определяемых уравнениями, полученными на основании свойства: логарифм единицы равен нулю.
пересекаются в точках, определяемых уравнениями, полученными на основании свойства: логарифм единицы равен нулю.
Таким образом, график функции  пересекается с осью
пересекается с осью  в точках, удовлетворяющих уравнению:
в точках, удовлетворяющих уравнению:
 ,
,
а график функции  - в точках, удовлетворяющих уравнению:
- в точках, удовлетворяющих уравнению:
 .
.
Решая эти уравнения графически, получим для каждого из них три действительных корня. Для уравнения  получим:
получим:  ,
,  и
и  , а для уравнения
, а для уравнения  получим:
получим:  ,
,  ,
,  . Принимая во внимание ОДЗ каждой функции и то, что
. Принимая во внимание ОДЗ каждой функции и то, что  , приходим к выводу, что функция
, приходим к выводу, что функция  пересекает ось
пересекает ось  в точках
в точках  и
и  , а функция
, а функция  - в точке
- в точке 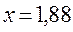 .
.
4.  Знаки функций.
Знаки функций.
 , если
, если 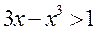 и
и  , если
, если  . Корни уравнения
. Корни уравнения  известны:
известны:  и
и  . Кривая знаков имеет вид (рис.12)
. Кривая знаков имеет вид (рис.12)
рис.13
Откуда заключаем:  , если
, если  и
и  , если
, если  и
и  .
.
Для функции  находим, что
находим, что  , если
, если  .
.
5. Вычисляем производные:

 Получаем:
Получаем:  .
.
Производная 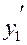 и
и  равна нулю в точках
равна нулю в точках  и
и  и не существуют в точках:
и не существуют в точках:  , которые не входят в ОДЗ, таким образом подозрительной на экстремум точкой является только
, которые не входят в ОДЗ, таким образом подозрительной на экстремум точкой является только  . Применяя теорему 3, найдем для малой окрестности
. Применяя теорему 3, найдем для малой окрестности  точки
точки  .
.
При  ,
, 
при  ,
,  .
.
При переходе через точку 
 меняет знак с " +" на " -", следовательно в точке
меняет знак с " +" на " -", следовательно в точке  функция имеет максимум:
функция имеет максимум:

6. а) На рассматриваемом промежутке  , в точках разрыва второго рода, исходная функция имеет вертикальные асимптоты, т.к.
, в точках разрыва второго рода, исходная функция имеет вертикальные асимптоты, т.к.

б) наклонные асимптоты: находим  , применяя правило Лопиталя:
, применяя правило Лопиталя:
 ;
;
Находим 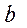 :
:  , т.е. не существует. Таким образом, данная функция не имеет наклонных асимптот, так как второй предел в (11) не существует.
, т.е. не существует. Таким образом, данная функция не имеет наклонных асимптот, так как второй предел в (11) не существует.
Все сказанное справедливо и для функции  .
.
7. Находим вторую производную
 Так как
Так как  всюду в ОДЗ, то дуги данной функции на любом интервале выпуклы.
всюду в ОДЗ, то дуги данной функции на любом интервале выпуклы.
Производные  и
и  не существуют в точках:
не существуют в точках: 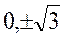 не входящих в ОДЗ и ни где не равны нулю, следовательно данная функция
не входящих в ОДЗ и ни где не равны нулю, следовательно данная функция  не имеет точек перегиба.
не имеет точек перегиба.
8. Составляя для удобства таблицу результатов исследования функции на интервале  :
:

| 
| 
| 
| 
| 
| 
| 
|

| - | + | + | + | - | - | + |
 
| |||||||

|
 Строим график для
Строим график для  , затем используя симметричность графика достраиваем его для
, затем используя симметричность графика достраиваем его для  . (рис. 13)
. (рис. 13)
Рис.14
Пример 5. 1. Функция определена при  или
или  , откуда получаем
, откуда получаем  и систему неравенств
и систему неравенств 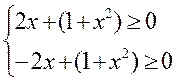 или
или  . Так как эти неравенства справедливы для любых
. Так как эти неравенства справедливы для любых  , то функция
, то функция 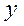 определена при всех
определена при всех  .
.
2. Функция нечетная, так как  .
.
Следовательно, график функции 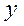 симметричен относительно начала координат, поэтому достаточно исследовать функцию при
симметричен относительно начала координат, поэтому достаточно исследовать функцию при  . Функция
. Функция 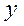 не является периодической.
не является периодической.
3. С осями координат график функции пересекается в начале координат – точке О  .
.
4. На рассматриваемом промежутке 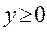 .
.
5. Найдем производную:
 Производная ни где не обращается в нуль и не существует в точках
Производная ни где не обращается в нуль и не существует в точках  и
и  .
.
На рассматриваемом отрезке подозрительном на экстремум является точка  . Используя теорему 3, получим для малой окрестности
. Используя теорему 3, получим для малой окрестности  точки
точки  :
:  при
при  и
и  при
при 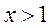 . Так как производная
. Так как производная  меняет знак с " +" на " -", то в точке
меняет знак с " +" на " -", то в точке  функция имеет максимум:
функция имеет максимум:
 .
.
Отметим, что так как в самой точке 
 не существует
не существует  , в этой точке максимум острый слева от точки
, в этой точке максимум острый слева от точки  на интервале
на интервале  ;
;  , и функция возрастает; Справа, на интервале
, и функция возрастает; Справа, на интервале  ,
,  , функция убывает.
, функция убывает.
6. а) Функция не имеет вертикальных асимптот, так как нет точек разрыва второго рода.
б) наклонные асимптоты:
 Таким образом функция имеет одну асимптоту
Таким образом функция имеет одну асимптоту  , которой является ось
, которой является ось  .
.
7. Вычислим  для
для 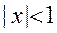 и
и  :
:

Вторая производная равна нулю при  и не существует в точках
и не существует в точках  , так как при этих значениях не существует
, так как при этих значениях не существует  .
.
Легко видеть, что  при
при  и
и  при
при 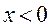 . Это означает, что слева от точки
. Это означает, что слева от точки  кривая вогнута, а справа – выпукла. Точка
кривая вогнута, а справа – выпукла. Точка  является абсциссой точки перегиба, а так как
является абсциссой точки перегиба, а так как  , то точка О(0, 0) является точкой перегиба. В рассматриваемом интервале
, то точка О(0, 0) является точкой перегиба. В рассматриваемом интервале 
 в интервале (0, 1) – здесь кривая выпукла;
в интервале (0, 1) – здесь кривая выпукла; 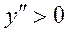 в интервале
в интервале  - здесь кривая вогнута. По определению точка
- здесь кривая вогнута. По определению точка  является абсциссой точки перегиба.
является абсциссой точки перегиба.
Так как  , то тогда
, то тогда  является точкой перегиба (и точкой максимума).
является точкой перегиба (и точкой максимума).
Сводя все результаты исследования в таблицу

| 
| 
| 
| 
|

| + | 
| + | |
 
| Не существ. | |||

| Не существ. |
Строим график функции (рис.15)
 |
 . Нахождение наибольших и наименьших значений функций на заданных отрезках или удовлетворяющих заданным условиям.
. Нахождение наибольших и наименьших значений функций на заданных отрезках или удовлетворяющих заданным условиям.
Известно, что непрерывная на отрезке  функция принимает наибольшее и наименьшее значение на этом отрезке либо в критических точках, либо на концах отрезка. Эти значения будем обозначать
функция принимает наибольшее и наименьшее значение на этом отрезке либо в критических точках, либо на концах отрезка. Эти значения будем обозначать  и
и  и отличать их от
и отличать их от  и
и  , так как вообще говоря это не одно и то же.
, так как вообще говоря это не одно и то же.
Решение задач нахождения  и
и  осуществляется по следующей схеме:
осуществляется по следующей схеме:
1. Находят критические точки функции, - точки из ОДЗ функции, в которых  или не существует.
или не существует.
2. Вычисляют значения функции во всех критических точках, лежащих внутри заданного отрезка и на его концах.
3. Сравнивают все вычисленные значения между собой и выбирают  и
и  .
.
Пример 1. Найти наибольшее и наименьшее значение функции  на отрезке
на отрезке  .
.
Решение: 1. Находим производную  и критические точки функции.
и критические точки функции.
 Из уравнения
Из уравнения  или
или  получаем точки
получаем точки 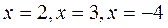 .
.
2. Вычисляем значения функции во всех этих точках:
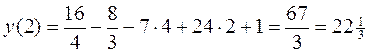

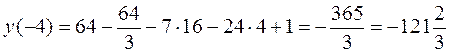
Значения функции на границах отрезка
 3. Сравнивая полученные значения функции, находим:
3. Сравнивая полученные значения функции, находим:


Ответ:  ,
,  .
.
Пример 2. Найти наибольшее и наименьшее значение функции 

На данном отрезке находятся точки:
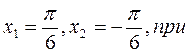
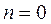


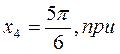
 .
.
Значения функции в этих точках:

Значения функции на границе отрезка:
 .
.
сравнивая все полученные значения, получим:


Ответ:  ,
, 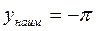 .
.
Часто встречаются задачи, в которых требуется найти значение какого-либо показателя, который определенным образом удовлетворяет некоторым поставленным условиям. Например требуется найти соотношение размеров цилиндрической цистерны, при котором полная поверхность цистерны была бы наименьшей (более дешевой) при заданном объеме. В связи с большим разнообразием подобных задач можно лишь отметить, что для их решения необходимо составить функцию, зависящую от нужного показателя и обычным образом найти точку, в которой эта функция достигает максимума или минимума (в зависимости от того, что требуют условия задачи), после чего с помощью достаточного признака надо убедиться в требуемом условиями задачи характер экстремума.
Пример1. Для доставки продукции завода  в город А (см. рис.) строиться строится шоссе
в город А (см. рис.) строиться строится шоссе  , соединяющее завод с железной дорогой (ЖД) и проходящей через город А и город В. Стоимость перевозок по шоссе вдвое больше, чем по ЖД. К какому пункту Р нужно подвести шоссе, чтобы общая стоимость перевозок продукции завода
, соединяющее завод с железной дорогой (ЖД) и проходящей через город А и город В. Стоимость перевозок по шоссе вдвое больше, чем по ЖД. К какому пункту Р нужно подвести шоссе, чтобы общая стоимость перевозок продукции завода  в город А по шоссе и по ЖД была бы наименьшей. Расстояние АВ=500км,
в город А по шоссе и по ЖД была бы наименьшей. Расстояние АВ=500км,  В=100км.
В=100км.
 |
Решение. В качестве показателя здесь удобно выбрать стоимость перевозки груза по пути  , часть АР этого пути груз провозится по ЖД, а часть пути
, часть АР этого пути груз провозится по ЖД, а часть пути  по шоссе.
по шоссе.
Пусть а – стоимость перевозки груза по ЖД на 1 км, тогда стоимость перевозки этого же груза на 1 км по шоссе будет 2а. Пусть  расстояние РВ (пункта Р от города В). Тогда стоимость перевозки груза по пути РА:
расстояние РВ (пункта Р от города В). Тогда стоимость перевозки груза по пути РА:
 ,
,
Стоимость перевозки груза по шоссе  :
:
 , т.к. длина пути
, т.к. длина пути  по теореме Пифагора
по теореме Пифагора  .
.
Общая стоимость перевозки груза от завода  до города А
до города А

является функцией переменного  , которое определяет расстояние пункта Р до города В.
, которое определяет расстояние пункта Р до города В.
Стоимость должна быть наименьшей, поэтому надо найти минимум этой функции. Находим производную:
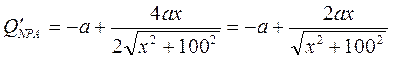
Приравниваем производную нулю:
 , откуда получаем
, откуда получаем  . Решая это уравнение, получим:
. Решая это уравнение, получим:

Таким образом пункт Р находится на расстоянии 57, 735 км от города В или на расстоянии 500-57, 735=442, 265(км) от города А.
Чтобы убедиться, что мы нашли минимум стоимости применим второй достаточный признак экстремума, для чего вычислим вторую производную:
 Видно, что
Видно, что  для любых
для любых  , а, следовательно, и для
, а, следовательно, и для  (км), т.е. мы действительно нашли минимум.
(км), т.е. мы действительно нашли минимум.
Ответ: Шоссе надо подвести к пункту Р, находящемуся от города А на расстоянии 442, 265км.
Пример 2. Суточные расходы при плавании судна состоят из двух частей: постоянной, равной а рублей, и переменной, возрастающей пропорционально кубу скорости  судна.
судна.
При какой скорости  плавание судна будет наиболее экономичным.
плавание судна будет наиболее экономичным.
Решение. Будем предполагать, что плавание будет продолжаться на некоторое расстояние  более, чем одни сутки.
более, чем одни сутки.
Из условия задачи следует, что суточные расходы 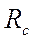 представляют собой функцию вида:
представляют собой функцию вида:
 , где
, где  коэффициент пропорциональности, с которым возрастает переменная составляющая суточных расходов. Пусть плавание судна продолжается
коэффициент пропорциональности, с которым возрастает переменная составляющая суточных расходов. Пусть плавание судна продолжается  суток, тогда расходы на все плавание составят:
суток, тогда расходы на все плавание составят:
 (руб.)
(руб.)
Очевидно, количество суток, которое займет плавание, будет зависеть от скорости судна  и, если судно должно преодолеть некоторое расстояние
и, если судно должно преодолеть некоторое расстояние  , то
, то 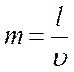 и расходы составят
и расходы составят  .
.
Найдем минимум этой функции:
 , поэтому
, поэтому  откуда получим
откуда получим  .
.
Убедимся, что при таком  расходы
расходы 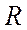 действительно минимальны (применяем второй достаточный признак экстремума).
действительно минимальны (применяем второй достаточный признак экстремума).
 .
.
В точке  ,
,
 легко видеть, что при
легко видеть, что при 
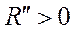 , т.к.
, т.к.  и
и  .
.
Следовательно, мы действительно нашли минимум расходов на плавание.
Ответ: Расходы на плавание будут минимальными, при скорости судна  .
.
Пример 3. Какой сектор следует вырезать из круга радиуса 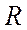 , чтобы из оставшейся части можно было свернуть воронку наибольшей вместимости.
, чтобы из оставшейся части можно было свернуть воронку наибольшей вместимости.
 |
Рис.16.
Решение: Обозначим угол вырезаемого сектора через  . Из оставшейся части можно свернуть конусообразную воронку с образующей
. Из оставшейся части можно свернуть конусообразную воронку с образующей  и длиной окружности ее основания, равной длине дуги АСВ круга (см.рис.16)
и длиной окружности ее основания, равной длине дуги АСВ круга (см.рис.16)
 .
.
Если обозначить радиус основания конуса через 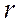 , то можно записать:
, то можно записать:
 , откуда получим
, откуда получим 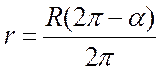 .
.
Вместимость (объем) воронки:
 , где
, где  - высота конуса, полученного при сворачивании сектора АСВ. Ее определим по теореме Пифагора.
- высота конуса, полученного при сворачивании сектора АСВ. Ее определим по теореме Пифагора.
 .
.
Объем воронки:
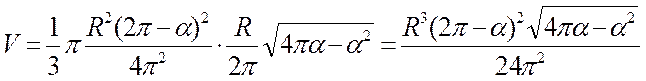
Найдем максимум этой функции:
 Приравнивая
Приравнивая  к нулю и преобразуя, получим уравнения для определения
к нулю и преобразуя, получим уравнения для определения  :
:
 , откуда находим:
, откуда находим:
 .
.
Так как  не может быть больше
не может быть больше  , то берем второй корень
, то берем второй корень  или в градусах
или в градусах  .
.
Убедимся, что в точке  действительно будет максимум функции
действительно будет максимум функции  .
.
Вычисляем вторую производную  .
.
 Подставляя сюда
Подставляя сюда  , получим:
, получим:
 .
.
Так как  , то в точке
, то в точке  функция
функция  достигает максимума.
достигает максимума.
Ответ: Наибольшая вместимость воронки получится, если из круга вырезать сектор с углом  , или в градусах
, или в градусах  .
.
Литература.
1. Г.М. Фихтенгольц. " Основы математического анализа" Т.1. Издательство " наука", М., 1964.
2. Н.С. Пикунов. " Дифференциальное и интегральное исчисления". Т.1. Издательство " Наука". М., 1976.
3. В. И. Смирнов. " Курс высшей математики". Т.1. Издательство " Наука". М., 1974.
4. М. С. Красс. " Математика для экономических специальностей". ИНФРА. М., 1998.
5. В. Е. Шнейдер и др. " Краткий курс высшей математики". Т.1. Издательство " Высшая школа". М., 1978.
Пример 2. Исследовать функцию  и построить ее график.
и построить ее график.
Решение: 1. ОДЗ: 
2. Функция общего вида.
3. График функции пересекается с осью 
 , когда
, когда  , т.е. в точке
, т.е. в точке  . С осью
. С осью 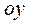
 график не пересекается, т.к.
график не пересекается, т.к.  не входит в ОДЗ функции.
не входит в ОДЗ функции.
Внутри ОДЗ – интервале  - точек разрыва функции нет.
- точек разрыва функции нет.
4. Так как  всюду в ОДЗ, то знак функции определяется знаком числителя. Так как
всюду в ОДЗ, то знак функции определяется знаком числителя. Так как 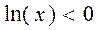 для
для  и
и  для
для 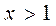 , то функция отрицательна на интервале
, то функция отрицательна на интервале  .
.
5. Для нахождения критических точек найдем производную  .
.


Производная существует всюду в ОДЗ и равна нулю, если  , т.е. в точке
, т.е. в точке 
 , если
, если  или
или 
 , если
, если  или
или  .
.
Таким образом, функция возрастает при  и убывает при
и убывает при  . При переходе через точку
. При переходе через точку  производная меняет знак с " +" на " -", следовательно,
производная меняет знак с " +" на " -", следовательно,  - точка, в которой функция достигает максимума.
- точка, в которой функция достигает максимума.

6. Уравнение вертикальной асимптоты  (ось
(ось 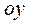 ), так как
), так как 
б) наклонные асимптоты:


 ,
, 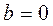
 - наклонная асимптота, т.е. наклонной асимптотой является ось
- наклонная асимптота, т.е. наклонной асимптотой является ось  .
.
8. Вычисляем 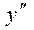 .
.

 , если
, если 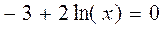 , т.е. при
, т.е. при 
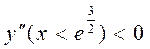 , т.е. кривая выпукла для
, т.е. кривая выпукла для 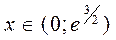 ,
,  , т.е. кривая вогнута для
, т.е. кривая вогнута для  .
.
Так как 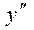 меняет знак при переходе через точку
меняет знак при переходе через точку  , то эта точка есть абсцисса точки перегиба:
, то эта точка есть абсцисса точки перегиба:  .
.
 .
.
Для построения графика функции сводим в таблицу результаты исследования.

| 
| 
| 
| 
| 
| 
| 
|
 
| 
| 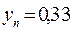
| |||||

| + | + | - | 
| - | ||

| - | -3 | - | 
| - | + |
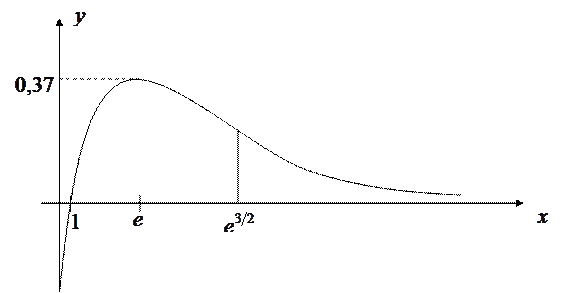 |
Рис.10.
Пример 3. Исследовать функцию  и построить ее график.
и построить ее график.
1. ОДЗ определяем из условия  , откуда
, откуда  ,
, 
т.е. ОДЗ является вся ось  кроме точек
кроме точек 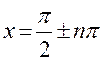 .
.
2. Функция  является периодической, четной (т.к. функция
является периодической, четной (т.к. функция 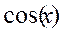 периодическая и четная). Период равен
периодическая и четная). Период равен  . График функции симметричен, поэтому для его построения достаточно исследовать функцию на отрезке
. График функции симметричен, поэтому для его построения достаточно исследовать функцию на отрезке  , и затем периодически продлить его на всю ось
, и затем периодически продлить его на всю ось  .
.
3. График функции пересекается с осью 
 в точке
в точке  . С осью
. С осью 
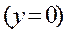 график ни где не пересекается, так как ни при каком конкретном
график ни где не пересекается, так как ни при каком конкретном 
 не равен нулю. Точки разрыва функции
не равен нулю. Точки разрыва функции  - точки разрыва второго рода.
- точки разрыва второго рода.
На рассматриваемом отрезке 
 , а
, а  и
и  , а
, а  .
.
4. Функция положительна при  и при
и при  и отрицательна при
и отрицательна при  .
.
5. Для нахождения экстремума вычислим  и
и 
 .
.
Суть понятия предела функции f(x) при xà x0 в том, что если он существует и равен числу b, то отличие функции от предела |b-f(x)| можно сделать сколь угодно малым, приближая x к x0. Сколь угодно малым означает, что это отличие будет меньше любого наперед заданного числа  > 0, как бы мало
> 0, как бы мало  не было. Иными словами: если всегда найдется x достаточно близкое к x0, при котором |b-f(x)|<
не было. Иными словами: если всегда найдется x достаточно близкое к x0, при котором |b-f(x)|<  , то число b есть предел функции f(x) при xà x0.
, то число b есть предел функции f(x) при xà x0.
Строгое понятие предела “на языке “ дает определение 1.
Пусть функция f (x) определена в некоторой окрестности точки x = x0, кроме, быть может, самой точки x0.
Число b называется пределом функции f(x) при xà x0, если для любого числа  > 0 как бы мало оно ни было, найдется такое число
> 0 как бы мало оно ни было, найдется такое число  > 0, что для всех x, удовлетворяющих условию 0< |b-f(x)|<
> 0, что для всех x, удовлетворяющих условию 0< |b-f(x)|<  , будет выполняться неравенство |b-f(x)|<
, будет выполняться неравенство |b-f(x)|<  .
.
В этом случае пишут:
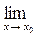 f (x)=b (1)
f (x)=b (1)
Из определения следует, что в самой точке x0, функция f(x) может быть не определена, то есть при образовании предела функции предельное значение x0 переменной x не учитывается. Это делает возможным сокращение под знаком предела при xà x0 множителей вида (xà x0), стоящих в числителе и в знаменателе, что удобно при вычислении пределов.
Особый интерес представляет случай, когда предел функции f(x) при xà x0 совпадает со значением функции в точке x0, т.е. когда
 f (x)à f (x0) (2)
f (x)à f (x0) (2)
В этом случае говорят, что функция f(x) непрерывна в точке x0; если же соотношение (2) нарушено, то говорят, что в точке x0 функция f(x) имеет разрыв.
Понятие производной базируется на понятии предела.
Определение 2. Производной функции y = f(x) в точке x0 называется предел отношения приращения функции в этой точке  y к приращению аргумента
y к приращению аргумента  x при стремлении приращения аргумента к нулю любым способом.
x при стремлении приращения аргумента к нулю любым способом.
Обозначается производная одним из символов y’(x0), f’(x0),  ; таким образом, можно записать
; таким образом, можно записать
 (3)
(3)
В общем случае производная является функцией и от неё так же можно находить производную, которую называют производной второго порядка (второй производной).
Вторую производную обозначают символами:
 ,
,  ;
; 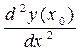 (4)
(4)
От второй производной можно находить третью производную и т.д.
К пределу (3) приводят многочисленные задачи в различных областях науки. В связи с этим существуют: механический смысл производной, геометрический смысл производной и т.п.
В экономике производная применяется для выражения предельных показателей: себестоимости и эластичности.
Поскольку себестоимость C произведенной продукции зависит от ее объема Q, то:
C = f (Q) (5)